Doppler effect of the rupture process of the great M_W7.9 Wenchuan earthquake

1.   Introduction

By taking more than seventy thousands lives and making billions of dollars' damage, the great M_W7.9 Wenchuan earthquake on May 12, 2008 shocked the world not only by seismic waves but also its damaging impact to the Chinese society. Scientists hare made great efforts to understand this great earthquake, including the tectonic background, fault structure and the rupture process, and etc. (Burchfiel et al., 2008). Although the surface rupture has been clearly observed in the field (Xu et al., 2009), arguments about the rupture process rose between unidirectional and bilateral after analyzing the teleseismic waveforms (Ji and Hayes 2008; Jin et al., 2008; Liu et al., 2008; Zhang et al., 2009). In this study, we investigate this problem by using a simple but effective approach for estimating the rupture direction, as well as other source parameters.

In the case of large earthquake, the fault plane usually develops into a long rectangle because the depth extent is limited by the thickness of the brittle seismogenic layer, which is usually less than 20 km. If the propagation of rupture is unidirectional, that is, the rupture starts from one end of the fault rupture plane and propagates to the other end, the spectrum and waveform of far field seismograms recorded at stations at a distance greater than 30° are shifted to higher frequency for the stations in the rupture propagation direction (Shearer, 1999) because of the Doppler effect, a phenomena discovered by Doppler in 1842.

For the spectrum of seismic displacement at far field, corner frequency is defined by the intersection of the asymptote of constant lower frequency component and the asymptote of the decaying higher frequency component. It is one of the important physical characters of seismic source described in text books of seismology. The value of corner frequency depends on the geometry of the fault plane, stress drop and magnitude of the earthquake and more importantly, the corner frequency also varies according to the azimuth from the source to the station if the rupture is unidirectional (Shearer, 1999). This phenomenon is related to the fact that the propagation speed of rupture on the fault plan is comparable to seismic velocity. As a result, the spectrum of seismic waveform at far field stations shifts to a higher frequency in the direction of rupture propagation and to a lower frequency in the direction opposite to the rupture propagation. This azimuth dependence could provide us additional independent information on the rupture process of a large earthquake such as the great M_W7.9 Wenchuan earthquake.

2.   Theory and method

In frequency domain the spectrum of a seismogram Y(ω) could be defined as

where S(ω), H(ω) and I(ω) stand for the source function, seismic wave propagation effect and the instrument response, respectively (Helmberger, 1983). After removing the instrument response I(ω) by deconvolution, we also need to consider the propagation effect of attenuation and geometrical radiation. For a far field seismic body wave, the propagation effect can be simplified as

where R is the ray distance, Q is a quality factor related to attenuation, v is the seismic wave velocity and F(R) is the geometrical spreading factor (Zhou and Xu, 2000). In this study, Q is assumed to be 500 and the travel time of a P phase is considered as R/v.

In the ω^-2 Haskell source model, the envelope of the source function S(ω) can be described as

where τ_c is the duration of the rupture, τ_r is the rise time, and M₀ is the earthquake moment. For the real seismograms, usually only one corner frequency can be identified as the intersection of ω^-0 and ω^-2 asymptotes, because the observed spectrum can be distorted by attenuation and near-surface effects (Shearer, 1999).

If the fault rupture surface of a large earthquake is a long rectangle (the length to depth ratio is larger than one) and the rupture is unidirectional, the corner frequency becomes azimuth anisotropic because of the Doppler effect, and this variation as a function of the azimuth angle can be described as

where f_L(ϕ) is the corner frequency at a far field station, is the real corner frequency, r_v is the ratio of the rupture propagation velocity to the seismic velocity, ϕ is the azimuth of the station to the epicenter and ϕ₀ is the rupture direction. As a result, the corner frequency should be higher at the rupture propagation direction and lower at the opposite direction.

By averaging the corner frequency at different azimuths, we could also estimate the size of the source (the rupture plane) from:

where r is the equivalent radius of the source, α is the seismic velocity and v is the rupture propagation velocity (Silver, 1983).

3.   Data and estimation of corner frequency

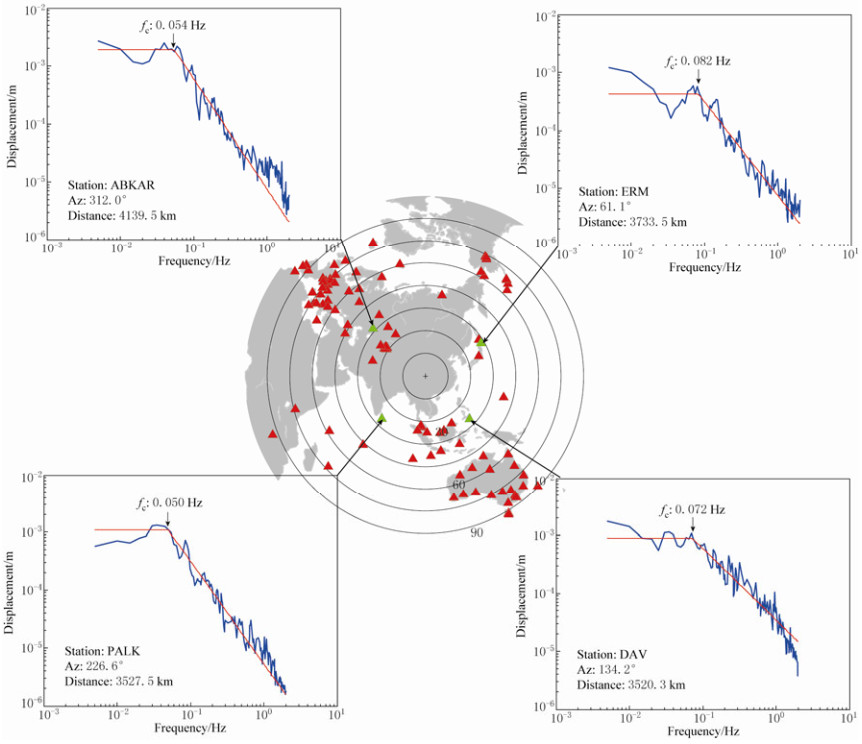
Seismic data from global broadband stations (Figure 1) have been downloaded from IRIS. We only used the data from stations more than 3 000 km from the epicenter, and applied a time window 10 s before and 200 s after the P arrival of the M_W7.9 Wenchuan earthquake. Before transforming the seismogram into frequency domain a careful manual selection is used to control the data quality.

Figure  1.  Station distribution (in the middle) and spectrum examples of the M_W7.9 Wenchuan earthquake at four different azimuths. The red lines are the square least fit result. Only the local maximum points in the spectrum are plotted.

DownLoad: Full-Size Img PowerPoint

The spectrum was then first three-point smoothed to reduce the noise, and only the local maximum points were used to estimate the envelope of the spectrum. We applied the non-linear least square method to fitting the spectrum envelope with three independent parameters: seismic moment, corner frequency and the power of ω in higher frequency. The corner frequency is limited in a reasonable range and the power of ω can vary from -1 to -3. A visual selection is also applied here to excluding the unqualified data.

After estimating the corner frequencies from different azimuths, we try to fit the curve described in equation (4) to get the real corner frequency, the rupture direction, and the ratio of rupture velocity to seismic velocity.

4.   Results and discussion

As shown in Figure 2, the corner frequency of the main shock of the Wenchuan earthquake is highly azimuth dependant, which implies that the rupture should be unidirectional. After using the equation (4) to fit the data we find that the rupture direction, which is determined by the highest corner frequency, is at the azimuth of 64.0°. And the earthquake mechanism given by the Global CMT Project suggested the fault plane striking at 49°, which agrees with our result with an a difference of about 15°.

Figure  2.  Corner frequency azimuth variation of the main shock of the M_W7.9 Wenchuan earthquake on May 12, 2008, obtained by fitting the spectrum according to Equation (4). The dominant rupture direction is at 64.0°, determined by the highest corner frequency.

DownLoad: Full-Size Img PowerPoint

Besides corner frequency, the phenomenon of Doppler effect can also be observed in the length of a P wavelet (Ni et al., 2005). As shown in Figure 3, the longest wavelet appears at the azimuth around 220°-240°, corresponding to the opposite direction of the rupture propagation.

Figure  3.  Azimuth variation of a P wavelet length. Waveforms are transformed into energy and stacked by azimuth. The azimuth around 220°-240° has the longest wavelet, corresponding to the opposite direction of the rupture propagation.

DownLoad: Full-Size Img PowerPoint

We have also applied the same technique to two major aftershocks of a magnitude of 6.0 and 5.8, respectively. However, we could not find any obvious variation of corner frequency on different azimuths (Figure 4). This result is reasonable because that the fault planes of smaller earthquakes are usually elliptical in shape or with an aspect ratio close to one, instead of long rectangles (aspect ratio of larger than one) where the rupture can propagate unidirectionally as shown in this study.

Figure  4.  Corner frequency of two aftershocks. (a) is for the earthquake on May 17th, 2008 with a magnitude 6.0 and (b) for an earthquake on May 25th, 2008 with a magnitude of 5.8.

DownLoad: Full-Size Img PowerPoint

We have demonstrated in this study that to observe the phenomenon of Doppler effect two critical condi tions must be satisfied. First, the earthquake must be big enough so that the length of the rupture plane is much larger than the width, (a larger aspect ratio), and the waveform can be clearly recorded by tele-seismic stations. Second, the rupture must propagate unidirectionally, from one end of the rupture surface to the other end.

The relationship between the geometry of rupture surface and earthquake magnitude can be presented by the following empirical formula (Wells and Coppersmith 1994),

where L is the length of rupture surface, and M_W is the moment magnitude of the earthquake. For an earthquake like the Wenchuan earthquake of magnitude 7.9, the rupture length at the surface was reported to be around 230 km. In the continent, the average continental seismogenic layer thickness is about 15 km. With the aspect ratio of about 15, the Doppler effect can be well observed for the M_W7.9 Wenchuan earthquake as reported here.

In the case of earthquakes with moment magnitude around 6, the length of rupture surface is ~12 km, which is comparable to the seismogenic layer thickness. Thus an earthquake with a magnitude smaller than 6 dose not to generate observable Doppler effect.

Other parameters obtained from the average of corner frequency and earthquake magnitude (from USGS) are listed in Table 1.

Table  1.  Source parameters of the M_W7.9 Wenchuan earthquake

 | Show Table

DownLoad: CSV

5.   Conclusions

Our analysis of the corner frequency variations shows that the great M_W7.9 Wenchuan earthquake had a dominating rupture propagation direction along 64.0°. We also estimated the equivalent radius of the fault rupture surface to be 33 km, yielding the rupture area of about 3 500 km². Therefore we estimate the length of the rupture surface to be about 230 km if the depth (or width) extent of 15 km for the rupture surface is assumed. Tthese results agree well with other studies within a reasonable accuracy. We also show that an earthquake with a magnitude smaller than 6 does not generate observable Doppler effect.

The computer program developed in this study can quickly provide us the information about the source of a future large (damaging) earthquake, which could be useful for predicting aftershocks and planning the rescue operations.