Diffraction of plane P waves by a canyon of arbitrary shape in poroelastic half-space (Ⅰ): Formulation

1.   Introduction

Earthquake observation and damage investigation have indicated that local site conditions, such as canyons and valleys, have significant effects on ground motion. Trifunac (1973) gave an exact solution for 2-D scattering of plane SH waves around a semi-cylindrical canyon, and then a lot of studies have been carried out on this subject. Among these studies there are analytical solutions (e.g., Wong and Trifunac, 1974; Cao and Lee, 1989, 1990; Lee and Cao, 1989; Todorovska and Lee, 1991; Yuan and Liao, 1994) and numerical solutions (e.g., Sanchez-Sesma and Rosenblueth, 1979; Wong, 1982; Kawase, 1988; Vogt et al, 1988; Bouchon, 1989; Sanchez-Sesma and Campillo, 1991; Liu and Liao, 1987; Zhang and Zhao, 1988; Liu and Han, 1991; Du et al, 1992; Liao, 2002; Cao et al, 2004; Zhou and Chen, 2007, 2008; Chen, 2007). The analytical method is often referred to as wave function expansion method, and the numerical methods include finite difference method, finite element method, boundary element method, discrete wave number method, wave source method, etc.

It should be noted that soil media are often saturated in reality. And analytical solutions for diffraction of plane P and SV waves around canyon in poroelastic half-space were obtained in reference (Li and Zhao, 2003, 2005; Liang et al, 2006), however, these solutions are approximate to a certain extent by introducing a very big circular-arc to imitate the surface of half-space (Lee and Liang, 2008).

In recent years, a special indirect boundary integration equation method (IBIEM), which has the advantages of reducing dimensions of problems, automatic satisfaction of boundary condition at infinite far, and high calculation precision, has been successfully applied in the field of diffraction of plane waves in elastic media (Sanchez-Sesma and Rosenblueth, 1979; Wong, 1982; Luco and de Barros, 1994; Dravinski and Mossessian, 1987). Based on the single-layer potential theory, the IBIEM resolves problems in the following way. Fictitious wave sources, by which scattered waves are constructed, are placed close to the boundaries of local topographies, and magnitude of the fictitious wave sources are determined by the boundary conditions. However, up to now the IBIEM method is still limited in elastic media, and it is valuable for the method to be extended to poroelastic media; also, the nature of diffraction of elastic waves around local topographies in poroelastic half-space needs to be studied in detail.

This paper, based on Biot's theory, derives the Green's functions of compressional and shear wave sources in poroelastic half-space, and presents formulation for the diffraction of plane P waves by a 2-D canyon of arbitrary shape in poroelastic half-space using the indirect boundary integration equation method. The precision of the method is verified by the satisfaction extent of boundary conditions, the comparison between the degenerated solutions of single-phased half-space and the well-known solutions, and the numerical stability of the method. The nature of diffraction of elastic waves around a canyon in poroelastic half-space is investigated in the companion paper (Liang and Liu, 2009a).

2.   Formulation

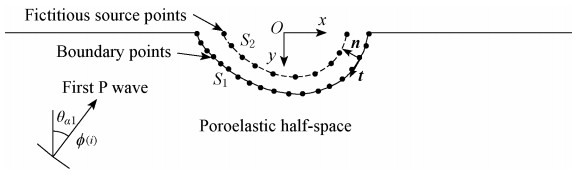
Figure 1 shows a canyon of arbitrary shape in poroelastic half-space. To construct scattered waves, fictitious sources are introduced close to the boundary S₁, forming a fictitious line S₂. The problem to be studied is the 2-D diffraction of plane P waves around the canyon of arbitrary shape in poroelastic half-space.

Figure  1.  The model

DownLoad: Full-Size Img PowerPoint

2.1   Biot's theory

If the displacement of the solid frame and the fluid displacement relative to the solid frame are denoted by u_i and w_i (i=x, y), respectively, the constitutive relations of a homogeneous poroelastic medium can be expressed as (Biot, 1941)

in which, σ_ij is total stress component of the bulk material, ε_ij and e are strain components and dilatation of the solid frame, respectively; λ and μ are Lame constants of the bulk material, p is pore pressure, δ_ij is Kronecker delta, α and M are Biot's parameters describing compressibility of the two-phased material, and 0≤ α ≤1 and 0≤ M < ∞.

The equations of motion of a homogeneous poroelastic medium can be expressed in terms of displacements u_i and w_i as (Biot, 1962)

and

where ρ= (1-n)ρ_s+nρ_f, ρ_s and ρ_f are mass density of the solid grain and the pore fluid, respectively, n is porosity of the solid frame; b is a parameter accounting for the internal friction due to the relative motion between the solid frame and the pore fluid, and b=0 if the internal friction is neglected; m is a density-like parameter depending on ρ_f and geometry of the pores.

Based on Biot's theory, there exist two compressional (P) waves and one shear (S) wave in poroelastic medium. Let k_α1, k_α2 and k_β denote the wave numbers for these waves, respectively, then for steady state response, the two P wave potentials ϕ₁ and ϕ₂ and the S wave potential ψ for the solid frame satisfy the following equations:

and

where is the Laplace operator defined by

Based on Helmholtz representation, the displacements of the solid frame and the fluid displacements relative to the solid frame for plane strain problem can be expressed as

where Φ and Ψ are the potentials for the pore fluid, and they satisfy the following equations:

and the parameters χ₁, χ₂ and χ₃ are given by

where λ_c=λ+α²M, ω is the frequency of motion, and c_α1 and c_α2 are the velocities for the two P waves, which are determined by

where

and the velocity for the S waves is c_β=μ/(ρ +ρ_fχ₃)^1/2.

2.2   Green's functions of compressional and shear wave sources buried in poroelastic half-space

To solve the problem, the Green's functions of compressional (P) and shear (SV) wave sources buried in half-space are needed. The Green's functions for the half-space can be obtained by the superposition of the potentials in full-space and by the satisfaction of boundary conditions at the surface of the poroelastic half-space (Lamb, 1904). This paper derives the Green's functions of compressional waves and shear wave buried in poroelastic half-space based on Biot's theory.

The boundary condition at the surface of the poroelastic half-space can be expressed as

The potentials for two P waves and SV wave due to the first P wave source at point (0, f ) can be expressed as

where H₀⁽²⁾(k_α1r₁) is the Hankel function of the second kind and of zero order; It is easy to verify that the potentials ϕ₁(x, y), ϕ₂(x, y) and Ψ(x, y) satisfy the equations (4a)-(4c) of wave motion.

The following integral representations (Lamb, 1904) for the Hankel functions are needed:

Define the dimensionless poroelastic parameters λ^*, M^*, ρ^*, m^* and b^*:

From the relations between the displacements and the potentials and from the boundary conditions the following equations in wave number (ξ) domain can be obtained for the drained case:

and

For the undrained case, only equation (16c) is replaced by

The unknowns A, B and C in the wave number domain can be resolved by the above equations, and the displacements and stresses can be obtained through Fourier transform.

The Green's functions of the second P wave and SV wave source at a point can be obtained in the same ways, and the detailed displacement and stress expressions for the Green's functions can be found in the reference (Liang and Liu, 2009b).

2.3   Wave fields

Based on Biot's theory, there exist two P waves and one SV wave in poroelastic medium. Suppose the first P wave is the incident wave, and the same below.

A plane first P wave with circular frequency ω and incident angle θ_α1 can be expressed as

where the time factor exp(iωt) is omitted here and thereafter.

In the absence of a canyon, the first P wave incident on the surface of the poroelastic half-space will generate one reflected first P wave, one reflected second P wave and one reflected SV wave, which can be expressed as (Lin et al, 2005)

and

in which, a₁, a₂ and b are reflection coefficients. The stress σ_f^ij, solid frame displacement u_i^f, fluid relative displacement w_i^f, and pore pressure p^f of the free field can be obtained, which can be found in the reference (Lin et al, 2005).

In the presence of a canyon, scattered waves are generated. In this paper, the scattered waves are constructed by fictitious wave sources placed close to the boundary of the canyon, and the displacements and stresses due to the scattered field can be expressed as

in which, b(x₂), c(x₂) and d(x₂) are amplitudes for the two P waves and the SV wave at position x₂ in fictitious line S₂; G_{i, l}^(u)(x, x₂), G_{i, l}^(w)(x, x₂), T_{ij, l}^(σ)(x, x₂) and T_l^(p)(x, x₂) are the Green's functions for solid frame displacement, fluid relative displacement, stress and pore pressure (subscript l =1, 2, 3 for first P wave, second P wave and SV wave sources, respectively).

Then the displacement field and stress field can be obtained by

2.4   Numerical solution

Because the Green's functions are for poroelastic half-space, the boundary conditions at the surface of the half-space are satisfied already, and only the boundary conditions at the surface of the canyon need to be considered. The boundary conditions at the surface of the canyon are

To obtain the numerical solution, it is necessary to discretize the boundary of the canyon, which is shown in Figure 1. If the number of the discrete boundary and that of the wave sources are N₁ and N₂ (N₁≥N₂), the displacement and stress of the scattered field can be written as

in which, x_n1∈S₁, x_n2∈S₂; n1=1, 2, …, N₁; n2=1, 2, …, N₂; b_n2, c_n2 and d_n2 are the amplitude of the first P wave, the second P wave and the SV wave at n2-th source, respectively.

It should be noted that the displacement and stress Green's functions above are derived in x-y coordinate system, and for canyon boundary of arbitrary shape it is necessary to make transformation. If the components of the unit normal vector at one discrete point of the canyon boundary are (l, m), the normal stress and tangent stress are

respectively, and the normal displacement of fluid is

Then from the boundary conditions (27), the following equations for the drained case are obtained

where x_n1∈S₁, x_n2∈S₂; n1=1, 2, …, N₁; n2=1, 2, …, N₂. And for the undrained case, only equation (36c) is replaced by

It should be noted that relevant Green's functions should be chosen for different drainage conditions.

Finally, the above equations can be written as

in which, H(3N₁, 3N₂) is the matrix of Green's function, Y(3N₂) is the vector to be solved, and F(3N₁) is the vector of free field. By using least-squares method the solution can be obtained by

in which, superscript ^* indicates the complex conjugate transpose.

If define residual

and it is easy to know that the smaller the residual is, the better the boundary conditions satisfy.

After the amplitudes of the wave sources are resolved, the total response in frequency domain can be obtained, the time-domain response can be calculated by Fourier transform then.

3.   Numerical implementation

Similar to single-phased medium, there exist singular integration points in wave number domain of the Green's functions of poroelastic half-space. When the internal friction parameter b≠0 or material damping of the medium is considered, the singular points will vanish. To consider the material damping, linear complex hysteretic damping is introduced by λ= λ(1+2ξi) and μ=μ(1+2ξi), in which, ξ is the damping ratio. After the material damping is taken into account, the upper limit of the integration can be much smaller. The Gaussion integration is used in this paper, in which, different integration intervals are used for different wave numbers.

Generally speaking, singularity appears if wave sources act on the canyon boundary. However, in this study the singularity is avoided because the wave sources are located at the fictitious line S₂ (close to but not on the canyon boundary S₁). Numerical experiments show that for incident frequencies η≤2.0 (η is the dimensionless frequency defined later) the wave sources should better be placed at the positions within 0.4-0.6 times of the relevant radii of the canyon, and the number of the wave sources can approximately take half of that of discrete points of canyon boundary; however, for higher incident frequency η > 2.0 the wave sources should be placed within 0.7-0.9 times of the relevant radii of the canyon, and the number of the wave sources can approximately take 0.8 times of that of discrete points of canyon boundary.

4.   Verification of accuracy

Accuracy of numerical results is verified for the case of a semi-circular canyon. Because there is no exact solution for the diffraction of plane waves by canyons in poroelastic half-space up to now, the verification is performed by three steps: the check of satisfaction extent of boundary conditions, the comparison between the degenerated solutions of single-phased half-space and the well-known solutions, and the numerical stability of the method.

Define the dimensionless incident frequency η=ωa/π(μ / ρ_s)^1/2, where a is radius of the canyon.

The check of boundary conditions shows that the stress residuals gradually decrease as the numbers of discrete points of the canyon boundary increase. Even for high incident frequency η=5.0, the normalized stress residual (normalized by the stress intensity of the incident P waves) can reach to a level of 10^-3 for N₁=81 and N₂=61, and to a level of 10^-4 for N₁=121 and N₂=101.

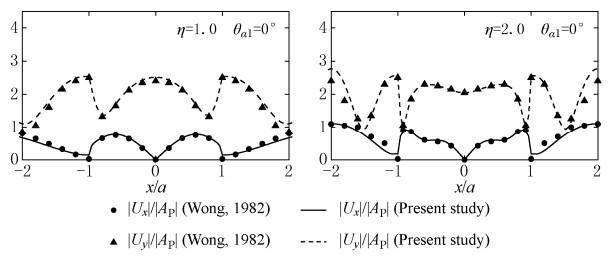
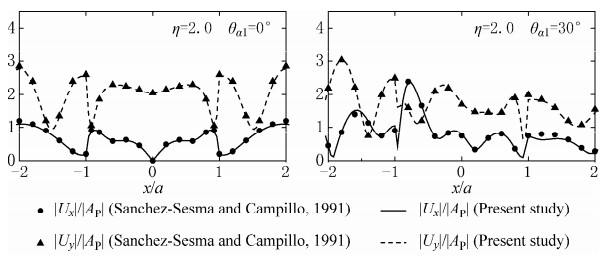
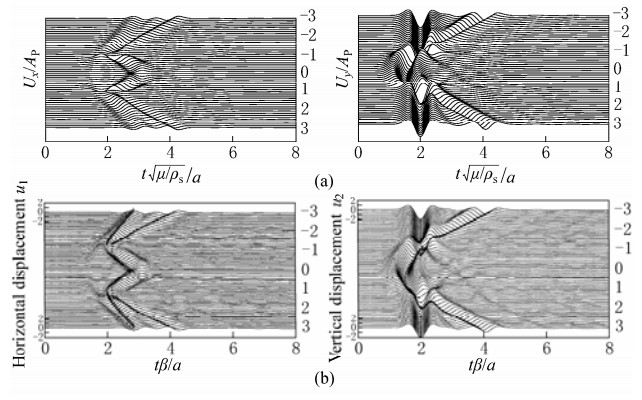
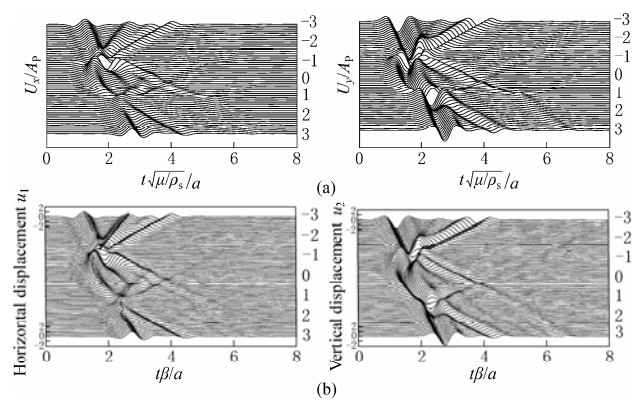
Figures 2 and 3 show the degenerated frequency responses around the canyon compared with the well known results of single-phased elastic half-space by Wong (1982) and Sanchez-Sesma and Campillo (1991) for incident frequency η=1.0 and 2.0, respectively. For the above degenerated solution, other parameters are taken as: porosity n =0.001, damping ratio ξ=0.001, and Poisson's ratio ν=1/3. Figures 4 and 5 show the degenerated time responses around the canyon for incident wave of Ricker wavelet (Ricker, 1977)

with the characteristic frequency f_c =ωa / 2π(μ/ρ_s)^1/2= 1.0 and the dimensionless time defined as τ= t (μ/ρ_s)^1/2/a, for incident angle θ_α1=0° and 30°, respectively, compared with the results of single-phased elastic half-space by Kawase (1988). Calculated frequencies are 100 in total, ranging from 0 to 3.0. Observation points are distributed at nearly equal intervals measured along the surface both inside and outside the canyon, and other parameters are taken for the degenerated solutions: porosity n =0.001, damping ratio ξ=0.001, and Poisson's ratio ν=1/3. It is shown that the results of this study are in excellent agreement with those in the references.

Figure  2.  Degenerated frequency solution compared with those of Wong (1982).

DownLoad: Full-Size Img PowerPoint

Figure  3.  Degenerated frequency solution compared with those of Sanchez-Sesma and Campillo (1991).

DownLoad: Full-Size Img PowerPoint

Figure  4.  Degenerated time solution for incident angle of 0° compared with those of Kawase (1988). (a) This paper; (b) Kawase's results.

DownLoad: Full-Size Img PowerPoint

Figure  5.  Degenerated time solution for incident angle of 30° compared with those of Kawase (1988). (a) This paper; (b) Kawase's results.

DownLoad: Full-Size Img PowerPoint

For numerical stability of the method, Table 1 gives the horizontal and vertical surface displacement amplitudes around the canyon versus the increase of the discrete points for incident frequency η =5.0. Other poroelastic parameters are λ^*=1.0, M^*=1.64, ρ^*=0.46, m^*=3.35, α =0.83, n =0.3, ν=0.25, and the numbers of the discrete points are taken as N₁=61, 81, 101, 121 and N₂=51, 61, 91, 101. From Table 1 it can be found that the surface displacement amplitudes converge very well as the increase on discrete points, which indicates the method has very good numerical stability even for very high incident frequency.

Table  1.  Numerical stability of displacement amplitudes for η =5.0

 | Show Table

DownLoad: CSV

5.   Conclusions

Based on Biot's theory, this paper derives the Green's functions of compressional and shear wave source in poroelastic half-space, and presents an indirect boundary integration equation method for diffraction of plane P waves by a two-dimensional canyon of arbitrary shape in poroelastic half-space. The precision of the method is verified by the check of boundary conditions, by the comparison between the degenerated solution and the well-known solutions, and by the numerical stability of the method. This method can also take into account the effect of the material damping. This study can be extended to layered poroelastic half-space if the relevant Green's functions of layered poroelastic half-space are used.