X
Advanced Search
Zhongxian Liu, Jianwen Liang (2010). Diffraction of plane P waves around an alluvial valley in poroelastic half-space. Earthq Sci 23(1): 35-43. DOI: 10.1007/s11589-009-0066-6
Citation: Zhongxian Liu, Jianwen Liang (2010). Diffraction of plane P waves around an alluvial valley in poroelastic half-space. Earthq Sci 23(1): 35-43. DOI: 10.1007/s11589-009-0066-6
shu

Diffraction of plane P waves around an alluvial valley in poroelastic half-space

  • Department of Civil Engineering, Tianjin University, Tianjin 300072, China

More Information
  • Corresponding author:

    Jianwen Liang, e-mail: liang@tju.edu.cn

  • Received Date: 20 Oct 2009
  • Accepted Date: 03 Dec 2009
  • Available Online: 30 May 2022
  • Published Date: 09 Feb 2010
    Abstract

  • Diffraction of plane P waves around an alluvial valley of arbitrary shape in poroelastic half-space is investigated by using an indirect boundary integral equation method. Based on the Green's functions of line source in poroelastic half-space, the scattered waves are constructed using the fictitious wave sources close to the interface of the valley and the density of fictitious wave sources are determined by boundary conditions. The precision of the method is verified by the satisfaction extent of boundary conditions, and the comparison between the degenerated solutions and available results in single-phase case. Finally, the nature of diffraction of plane P waves around an alluvial valley in poroelastic half-space is investigated in detail through numerical examples.

    • FullText(HTML)

  • It is well known that alluvial valleys may result in large amplification of ground motion during earthquakes. In the early 1970s, developed an exact solution for diffraction of plane SH waves around a semi-cylindrical alluvial valley. Then many studies have been made on this topic. In these studies there are analytical solutions (e.g., ; ; ) and numerical solutions (e.g., ; ; ; ; ; ). The analytical method is often referred to as wave function expansion method, and the numerical method includes finite difference method, finite element method, boundary element method, discrete wave number method, wave source method, etc.

    It should be noted that soil media are often saturated in reality, especially in coastal region. and studied diffraction of elastic waves around a valley in poroelastic half-space using wave function expansion method and complex function method, respectively. However, in these studies there exists an approximation to some extent by introducing a very big circular-arc to imitate the surface of half-space ().

    In recent years, a special indirect boundary integral equation method (IBIEM) has been applied to the field of diffraction of plane waves in elastic media (; ; ), and has been extended to the case of poroelastic media by , ). It is illustrated that this method has several advantages, such as reducing dimensions of problems, automatic satisfaction of radiation condition, and high calculation precision. Based on Green's function by , this method is further extended to the solution for diffraction of elastic waves around alluvial valleys in poroelastic half-space. The nature of diffraction of plane P waves around an alluvial valley is investigated in detail through numerical examples, and some conclusions are obtained.

    2.1   Model

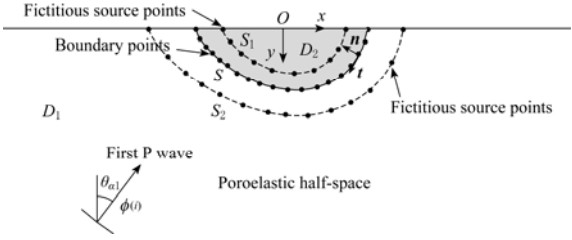
    The problem to be studied is the 2-D diffraction of plane P waves around an alluvial valley of arbitrary shape in poroelastic half-space, as shown in Figure 1. Both the half-space (D1) and the valley (D2) are assumed to be poroelastic, homogeneous and isotropic. The symbol S refers to the interface between the half-space and the valley. To construct the diffracted waves in the half-space and the valley, fictitious wave sources are introduced close to the interface S, forming two fictitious surfaces S1 and S2, inside and outside the valley, respectively.

    Figure 1. The model.
    Figure  1.  The model.
    DownLoad: Full-Size Img PowerPoint

    2.2   Biot's theory

    If the displacement of the solid frame and the fluid displacement relative to the solid frame are denoted by ui and wi (i=x, y), respectively, the constitutive relations of a homogeneous poroelastic medium can be expressed as ()

    		(1)

    		(2)

    in which, σij is total stress component of the bulk material, εij and e are strain components and dilatation of the solid frame, respectively; λ and μ are Lame constants of the bulk material, p is pore pressure, δij is Kronecker delta, α and M are Biot's parameters describing compressibility of the two-phase material, and 0≤α≤1 and 0≤M≤∞.

    The motion equations of a homogeneous poroelastic medium can be expressed in terms of displacements ui and wi as ()

    		(3)

    		(4)

    where and ρf are mass density of the solid grain and the pore fluid, respectively, n is porosity of the solid frame; b is a parameter accounting for the internal friction due to the relative motion between the solid frame and the pore fluid, and b=0 if the internal friction is neglected; m is a density-like parameter depending on ρf and the geometry of the pores.

    Based on Biot's theory, there exist two compressional (P) waves and one shear (S) wave in poroelastic medium. Let kα1, kα2 and kβ denote the wave numbers for these waves, respectively, then for steady-state response, the two P wave potentials ϕ1 and ϕ2 and the S wave potential ψ for the solid frame satisfy the following equations:

    		(5a)

    		(5b)

    and

    		(5c)

    where is the Laplace operator defined by

    To clarify the waves in D1 and D2, the wave numbers of two P waves and SV wave are represented by kα11, kα21, kβ1 in half-space, respectively, and kα12, kα22 and kβ2 for the alluvial valley, correspondingly.

    2.3   Wave fields

    2.3.1   Free field

    Consider a poroelastic half-space subjected to incident plane first P waves, the potentials of incident waves can be expressed by

    		(6)

    where θα1 represents the incident angle. The time factor exp(iωt) is omitted here and thereafter. The first P wave incident on the surface of the poroelastic half-space will generate one reflected first P wave, one reflected second P wave and one reflected SV wave, which can be expressed as ()

    		(7)

    		(8)

    		(9)

    where a1, a2 and b are reflection coefficients. The stress σijf, solid frame displacement uif, fluid relative displacement wif, and pore pressure pf of the free field can be obtained.

    2.3.2   Diffracted waves

    In the presence of the alluvial valley, diffracted waves are generated. In this paper, the diffracted waves inside and outside the alluvial valley are constructed by fictitious wave sources placed on the surfaces S1 and S2, respectively.

    The displacements and stresses in the half-space due to the diffracted wave field can be expressed as

    		(10)

    		(11)

    		(12)

    		(13)

    in which, x∈D1, x1∈S1; b(x1), c(x1) and d(x1) are the amplitudes for the two P waves and the SV wave at position x1 in the fictitious surface S1; , are the Green's functions for solid frame displacement, fluid relative displacement, stress and pore pressure in the half-space (subscript l=1, 2, 3 for first P wave, second P wave and SV wave sources, respectively). These Green's functions already satisfy the wave motion equation and the boundary condition of free surface. The expression of these Green's functions can be found in paper ().

    Then the displacement field and stress field in the half-space can be obtained by

    		(14a)

    		(14b)

    		(14c)

    and

    		(14d)

    In the same way, the displacements and stresses in the alluvial valley can be expressed as

    		(15)

    		(16)

    		(17)

    		(18)

    in which, x∈D2, x2∈S2; e(x2), f (x2) and g(x2) are the amplitudes for the two P waves and the SV wave at position x2 in the fictitious surface S2; , are the Green's functions for solid frame displacement, fluid relative displacement, stress and pore pressure in the alluvial valley.

    2.4   Boundary condition

    The boundary conditions of this problem include traction free conditions on the surface of the half-space, and the continuity conditions along the interface S. Because the boundary conditions at the surface of the valley and the half-space are satisfied already, only the continuity boundary conditions need to be considered.

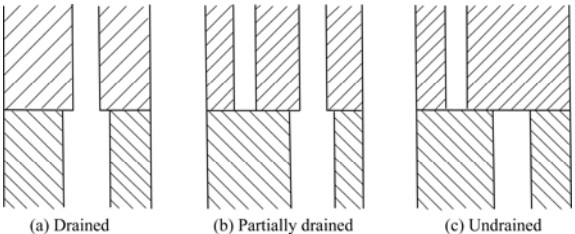
    The drained and undrained conditions at the interface are usually assumed for such problem (Figures 2a and 2c). However, the partially drained condition is more common in reality (Figure 2b). Based on the work of , the boundary conditions are defined as

    Figure 2. Drainage conditions at the interface (Deresiewicz, 1963).
    Figure  2.  Drainage conditions at the interface ().
    DownLoad: Full-Size Img PowerPoint

    		(19a)

    		(19b)

    		(19c)

    where superscript "s" and "v" represent the half-place and the alluvial, respectively; the symbol k is a coefficient of resistance, which represents a measure of restriction of the flow across the interface resulting from imperfect alignment of the interfacial pores; is the normal component of the relative velocity of liquid with respect to solid phase. For two limiting cases, equation (19c) can be reduced to

    		(20a)

    or

    		(20b)

    To obtain the numerical solution, it is necessary to discretize the interface S and the wave source surfaces S1 and S2, which is shown in Figure 1. If the numbers of the discrete points on the surfaces S, S1 and S2 are N, N1 and N2 (N≥N1, N≥N2), respectively, the displacement and stress of the scattered field in the half-space can be written as

    		(21)

    		(22)

    		(23)

    		(24)

    where and dn1 are the densities of the first P wave, the second P wave and the SV wave at n1th source, respectively.

    As for the wave field inside the alluvium, the surface S2 can be discretized in the same way, and the densities of the first P wave, the second P wave and the SV wave at n2th source on S2 can be denoted by en2, fn2 and gn2.

    Then from the boundary conditions (19), the following equations can be obtained:

    		(25)

    in which, H1(6N, 3N1), H2(6N, 3N2) are influence matrix which corresponds to the displacement and stress due to fictitious wave sources on the surface S1, S2, respectively. Y1(3N1, 1) and Y2(3N2, 1) are unknown density vector. F(6N, 1) is the displacement and stress vector of free field. The equation can be solved by using least-squares method. Once the unknown wave source density is calculated, the whole wave field can be obtained through superposition of diffracted field and free field.

    Compared with other boundary integral equation methods, one prominent character of this method is that the singularity is avoided because the wave sources are located at the fictitious surface S1 (close to but not on the valley boundary S). The numerical experiments show that at least seven discrete points per wave-length are required on the boundary. For incident frequency η≤2.0 (η is the dimensionless frequency defined later) the number of the wave sources can approximately take 0.5−0.8 times the number of discrete points of valley boundary, and the wave sources should better be placed within 0.4−0.6 times of the relevant radii of the valley; however, for higher incident frequency η > 2.0 the wave sources should be placed within 0.7-0.9 times of the relevant radii of the valley, and the number of the wave sources can approximately take 0.8-0.9 times of that of discrete points of valley boundary. For convenience, S1 and S2 follow the shape of S, and the distances between S2 and S are identical to those between S1 and S.

    It is worth noting that the Green's functions of line source in poroelastic half-space are computed by Fourier transformation in space-wave number domain. To consider the material damping, linear complex hysteretic damping is introduced by , in which, ζ is the damping ratio. Then the seven-point Gaussian integration is used to compute the Green's function in this paper, in which, different integration intervals are used for different incident frequency to improve the computation efficiency. It should be noted that for η=2 (N=41, N1=25), the computation can be completed within 10 minutes on a common personal computer with CPU 2.40 GHz and memory 2.0 Gb.

    Accuracy of numerical results is verified for the case of a semi-circular alluvial valley. Because there is no exact solution for the diffraction of plane waves by an alluvial valley in poroelastic half-space up to now, the verification is performed by the check of satisfaction extent of boundary conditions and the comparison between the degenerated solutions of single-phase halfspace and the well-known solutions.

    The dimensionless incident frequency is defined as , where a is radius of the valley, cβ is the shear wave velocity in half-space.

    The check of boundary conditions shows that the stress residuals gradually decrease as the number of discrete points of the interface increases. Even for high incident frequency η=3.0, the normalized stress residual (normalized by the stress intensity of the incident P waves) can reach to a level of 10-3 for N=81 and N1=61.

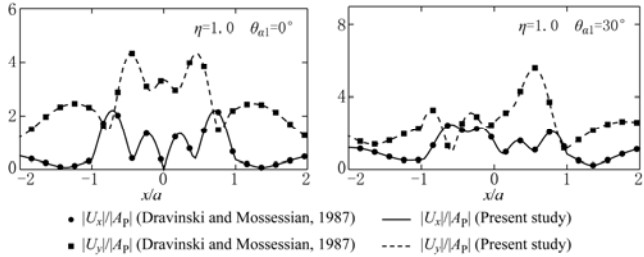
    For the degenerated solution of single-phase half-space, the following parameters associated with poroelasticity are taken: M*=ρf*=m*=α=0, and with the shear modular ratio μ*=1/6, the damping ratio ζ=0.001, Poisson's ratio v=1/3 and incident frequency η=1.0. Figure 3 shows the surface displacement amplitudes of the half-space compared with the well-known results of single-phase half-space by for incident angle θα1=0° and θα1=30°, respectively. It is shown that the results in the present study are in excellent agreement with the results of .

    Figure 3. Degenerated frequency solution compared with the results of Dravinski and Mossessian (1987).
    Figure  3.  Degenerated frequency solution compared with the results of .
    DownLoad: Full-Size Img PowerPoint

    The parameters of saturated poroelastic media in the half-space are defined as follows: Poisson's ratio v= 0.25, porosity ns= 0.3, the bulk modulus of the solid grain Kgs=36 GPa, the bulk modulus of fluid Kf =2 GPa, the mass density of the solid grain ρs=2.65×103 kg/m3, the mass density of fluid ρf =1.0×103 kg/m3. The corresponding parameters are taken: λ*=1.0, M*=1.64, ρ*=0.46, M*=3.35, α*=0.28. The material parameters of saturated poroelastic medium inside the valley are listed in Table 1 for different porosities ( ). It should be noted that the bulk modulus of the solid grain Kgv=9 GPa, the critical bulk modulus of the solid frame Kcr=50 MPa, and the critical porosity ncr=0.36. The linear hysteretic damping ratio ζ=0.001 is used for the following study.

    Table  1.  Properties of poroelastic medium inside the valley for different porosities
     | Show Table
    DownLoad: CSV

    Figures 4 to 6 illustrate the horizontal and vertical surface displacement amplitudes near the valley in a dry poroelastic half-space, drained poroelastic half-space and undrained poroelastic half-space, respectively, for porosity ns=0.3 and nv=0.3, dimensionless incident frequency η=0.5, 1.0, and 2.0, and incident angle θα1=0°, 30°, 60° and 85°, respectively. The surface displacement amplitudes are normalized by the displacement amplitude of the incident P wave. It is shown that the surface displacement amplitudes of the dry case are significantly different from those of the saturated (either drained or undrained) cases, and the drainage condition has large effect on the surface displacement amplitude; the displacement amplitudes of the dry case are usually larger than that of the undrained case, and the displacement amplitudes of the undrained case are usually larger than that of the drained case. From these figures phase shift can also be easily observed between the dry case and the saturated cases, as well as the slightly longer resultant wavelengths for the undrained case than those for the drained case and the longer resultant wavelengths for the drained case than those for the dry case.

    Figure 4. Surface displacement amplitudes of dry poroelastic, drained poroelastic, and undrained poroelastic half-spaces (η=0.5, ns=0.3, nv=0.3).
    Figure  4.  Surface displacement amplitudes of dry poroelastic, drained poroelastic, and undrained poroelastic half-spaces (η=0.5, ns=0.3, nv=0.3).
    DownLoad: Full-Size Img PowerPoint
    Figure 5. Surface displacement amplitudes of dry poroelastic, drained poroelastic, and undrained poroelastic half-spaces (η=1.0, ns=0.3, nv=0.3).
    Figure  5.  Surface displacement amplitudes of dry poroelastic, drained poroelastic, and undrained poroelastic half-spaces (η=1.0, ns=0.3, nv=0.3).
    DownLoad: Full-Size Img PowerPoint
    Figure 6. Surface displacement amplitudes of dry poroelastic, drained poroelastic, and undrained poroelastic half-spaces (η=2.0, ns=0.3, nv=0.3).
    Figure  6.  Surface displacement amplitudes of dry poroelastic, drained poroelastic, and undrained poroelastic half-spaces (η=2.0, ns=0.3, nv=0.3).
    DownLoad: Full-Size Img PowerPoint

    Figures 7 illustrates the horizontal and vertical surface displacement amplitudes near the valley under different drainage condition on interface S (the flat ground surface is assumed to be drained), for η=0.5, 1.0 and 2.0, and for k=0 (drained), 5, 10, 20, and ∞ (undrained), respectively, in which, the case 0 < k < ∞ corresponds to the condition of partially drained. Other parameters are identical to the above examples. As shown in these figures, with the increase of the resistance coefficient, the displacement amplitudes gradually approach to that of the undrained case. From these results, it may be suggested that k=5 may be approximately defined as semi-drained condition in this study.

    Figure 7. Surface displacement amplitude near the valley with variation of resistance coefficient k (ns=0.3, nv=0.3).
    Figure  7.  Surface displacement amplitude near the valley with variation of resistance coefficient k (ns=0.3, nv=0.3).
    DownLoad: Full-Size Img PowerPoint

    Figure 8 illustrates the surface pore pressures along the interface between the valley and the half-space (undrained conditions at the interface and the ground surface), for porosity ns=0.3 and nv=0.3, Poisson's ratio v=0.25. The surface pore pressures are normalized by the stress intensity of the incident P wave. It can be seen from Figure 8 that large pore pressures occur along the interface, and the pore pressures depend strongly on the incident angle and the incident frequency. The pore pressures are smooth along the interface for the lower incident frequency and become more complicated with the increase of the incident frequency, which suggests that the higher-frequency waves more easily stimulate pore pressures of large amplitudes and of rapid oscillations.

    Figure 8. Pore pressure around the interface under different incident angles for undrained boundary (ns=0.3, nv=0.3).
    Figure  8.  Pore pressure around the interface under different incident angles for undrained boundary (ns=0.3, nv=0.3).
    DownLoad: Full-Size Img PowerPoint

    Figures 9 to 11 and Figures 12 to 14 illustrate the normalized horizontal and vertical displacement amplitudes around the valley, for drained and undrained boundary conditions, respectively. The parameters are defined as follows: porosity ns=0.3 and nv=0.3, 0.34 and 0.36, Poisson's ratio v=0.25, dimensionless incident frequency η=0.5, 1.0 and 2.0, and incident angle θα1=0°, 30°, 60° and 85°, respectively. It can be seen from these figures that the porosity of the valley has significant effect on the surface displacement amplitudes both for the drained and undrained cases. As the increase of the porosity of the valley, the surface displacement amplitudes increase and the surface displacement amplitude gradually become complicated with rapid oscillation, especially for the case of critical porosity and for higher incident frequency.

    Figure 9. Surface displacement amplitude for different porosities for drained boundary (η=0.5, ns=0.3).
    Figure  9.  Surface displacement amplitude for different porosities for drained boundary (η=0.5, ns=0.3).
    DownLoad: Full-Size Img PowerPoint
    Figure 10. Surface displacement amplitude for different porosities for drained boundary (η=1.0, ns=0.3).
    Figure  10.  Surface displacement amplitude for different porosities for drained boundary (η=1.0, ns=0.3).
    DownLoad: Full-Size Img PowerPoint
    Figure 11. Surface displacement amplitude for different porosities for drained boundary (η=2.0, ns=0.3).
    Figure  11.  Surface displacement amplitude for different porosities for drained boundary (η=2.0, ns=0.3).
    DownLoad: Full-Size Img PowerPoint
    Figure 12. Surface displacement amplitude for different porosities for undrained boundary (η=0.5, ns=0.3).
    Figure  12.  Surface displacement amplitude for different porosities for undrained boundary (η=0.5, ns=0.3).
    DownLoad: Full-Size Img PowerPoint
    Figure 13. Surface displacement amplitude for different porosities for undrained boundary (η=1.0, ns=0.3).
    Figure  13.  Surface displacement amplitude for different porosities for undrained boundary (η=1.0, ns=0.3).
    DownLoad: Full-Size Img PowerPoint
    Figure 14. Surface displacement amplitude for different porosities for undrained boundary (η=2.0, ns=0.3).
    Figure  14.  Surface displacement amplitude for different porosities for undrained boundary (η=2.0, ns=0.3).
    DownLoad: Full-Size Img PowerPoint

    Based on the Green's functions of line source in poroelastic half-space, the diffraction of plane P waves around an alluvial valley is solved by the indirect boundary integration equation method in this paper. The nature of diffraction of plane P waves around an alluvial valley was investigated, and the effects of drainage condition, porosity, incident frequency and incident angle on the diffraction of waves were studied in detail. Some conclusions are obtained.

    Surface displacement amplitudes of the dry case are significantly different from those of the saturated (either drained or undrained) cases, and the drainage condition has large effect on the surface displacement amplitude; the displacement amplitudes of the dry case are usually larger than that of the undrained case, and the displacement amplitudes of the undrained case are usually larger than that of the drained case. Phase shift can be easily observed between the dry case and the saturated cases, as well as the slightly longer resultant wavelengths for the undrained case than those for the drained case and the longer resultant wavelengths for the drained case than those for the dry case. Porosity of the valley has significant effect on the surface displacement amplitudes both for the drained and undrained cases. As the increase of the porosity of the valley, the surface displacement amplitudes increase and the surface displacement amplitude gradually become complicated with rapid oscillation.

    It should be noted that the numerical examples are implemented for a semi-circular alluvial valley. However, this method can be used for alluvial valley of arbitrary shape. Moreover, it is convenient for this method to be used for the case of layered half-space with the corresponding dynamic Green's function.

    This work is supported by National Natural Science Foundation of China (50978183).

    • References (22)
  • Biot M A (1941). General theory of three-dimensional consolidation. J Appl Phys 12(2): 155-164. doi: 10.1063/1.1712886
    Biot M A (1962). Mechanics of deformation and acoustic propagation in porous media. J Appl Phys 33(4): 1 482-1 498. doi: 10.1063/1.1728759
    Boore D M, Larner K L and Aki K (1971). Comparison of two independent methods for the solution of wave scattering problems: response of a sedimentary basin to incident SH waves. J Geophys Res 76: 558-569. doi: 10.1029/JB076i002p00558
    de Barros F C P and Luco J E (1995). Amplification of obliquely incident waves by a cylindrical valley embedded in a layered half-space. Soil Dynam Earthq Eng 14(3): 163-175. doi: 10.1016/0267-7261(94)00047-K
    Deresiewicz H (1963). On uniqueness in dynamic poroelasticity. Bull Seism Soc Amer 53: 595-626. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/53/4/783/116181/on-uniqueness-in-dynamic-poroelasticity?redirectedFrom=fulltext
    Dravinski M and Mossessian T K (1987). Scattering of plane harmonic P, SV, and Rayleigh waves by dipping layers of arbitrary shape. Bull Seism Soc Amer 77: 212-235. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/77/1/212/118927/scattering-of-plane-harmonic-p-sv-and-rayleigh?redirectedFrom=fulltext
    Du X L, Xiong J G and Guan H M (1993). Boundary integration equation method to scattering of plane SH waves. Acta Seismologica Sinica 6(3): 609-618. doi: 10.1007/BF02650400
    Kawase H and Aki K (1989). A study on the response of a soft basin for incident P, S, Rayleigh waves with special reference to the long duration observed in Mexico city. Bull Seism Soc Amer 78: 1 361-1 382. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/79/5/1361/119226/a-study-on-the-response-of-a-soft-basin-for?redirectedFrom=fulltext
    Lee V W and Liang J (2008). Free-field (elastic or poroelastic) half-space zero-stress or related boundary conditions. Proceedings of 14th World Conference on Earthquake Engineering. Beijing, October 12-17, Paper 03-03-0002.
    Li W H, Zhao C G and Shi P X (2005). Scattering of plane P waves by circular-arc alluvial valleys with saturated soil deposits. Soil Dynam Earthq Eng 25: 997-1 014. doi: 10.1016/j.soildyn.2004.10.010
    Liang J and Liu Z (2009a). Diffraction of plane P waves by a canyon of arbitrary shape in poroelastic half-space (Ⅰ): Formulation. Earthquake Science 22(3): 215-222. doi: 10.1007/s11589-009-0215-y
    Liang J and Liu Z (2009b). Diffraction of plane SV waves by a cavity in poroelastic half-space. Earthq Eng Eng Vib 8(1): 29-46. doi: 10.1007/s11803-009-8077-9
    Liao Z P (2002). Introduction to Wave Motion Theories in Engineering. Science Press, Beijing, 236-270 (in Chinese).
    Lin C H, Lee V W and Trifunac M D (2005). The reflection of plane waves in a poroelastic half-space fluid saturated with inviscid fluid. Soil Dynam Earthq Eng 25: 205-223. doi: 10.1016/j.soildyn.2004.10.009
    Sanchez-Sesma F J, Ramos-Martinez J and Campillo M (1993). An indirect boundary element method applied to simulate the seismic response of alluvial valleys for incident P, S and Rayleigh waves. Earthq Eng Struct Dynam 22: 279-295. doi: 10.1002/(ISSN)1096-9845
    Todorovska M and Lee V W (1991). Surface motion of shallow circular alluvial valleys for incident plane SH waves: Analytical solution. Soil Dynam Earthq Eng 10: 192-200. doi: 10.1016/0267-7261(91)90033-V
    Trifunac M D (1971). Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves. Bull Seism Soc Amer 61: 1 755-l 770. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/61/6/1755/117035/surface-motion-of-a-semi-cylindrical-alluvial?redirectedFrom=fulltext
    Wong H L (1982). Effect of surface topography on the diffraction of P, SV, and Rayleigh waves. Bull Seism Soc Amer 72: 1 167-1 183. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/72/4/1167/118334/effect-of-surface-topography-on-the-diffraction-of?redirectedFrom=fulltext
    Wong H L and Trifunac M D (1974). Surface motion of a semi-elliptical alluvial valley for incident plane SH waves. Bull Seism Soc Amer 64: 1 389-1 408.
    Yuan X M and Liao Z P (1995). Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section. Earthq Eng Struct Dynam 24: 1 303-1 313. doi: 10.1002/(ISSN)1096-9845
    Zhou H and Chen X F (2008). The localized boundary integral equation-discrete wave number method for simulating P-SV wave scattering by an irregular topography. Bull Seism Soc Amer 98(1): 265-279. doi: 10.1785/0120060249
    Zhou X L, Jiang L F and Wang J H (2008). Scattering of plane wave by circular-arc alluvial valley in a poroelastic half-space. J Sound Vib 318(4-5): 1 024-1 049. doi: 10.1016/j.jsv.2008.04.057
    • Related Articles

  • Related Articles

    Chenrui He, Zhongxian Liu, Lei Liu. 2019: The scattering of plane P1 wave by a 3-D sedimentary basin in a fluid-saturated poroelastic half-space using IBEM. Earthquake Science, 32(3-4): 143-156. DOI: 10.29382/eqs-2019-0143-05
    Heather P. Brandow, Vincent Lee. 2018: Weighted residual method for diffraction of plane P-waves in a 2-D elastic half-space III: on an almost circular arbitrary-shaped alluvial valley. Earthquake Science, 31(1): 19-34. DOI: 10.29382/eqs-2018-0003-3
    Jianwen Liang, Bing Han, Zhenning Ba. 2013: 3D Diffraction of obliquely incident SH waves by twin infinitely long cylindrical cavities in layered poroelastic half-space. Earthquake Science, 26(6): 395-406. DOI: 10.1007/s11589-013-0046-8
    Zhenning Ba, Jianwen Liang, Xiongyi Mei. 2013: 3D scattering of obliquely incident plane SV waves by an alluvial valley embedded in a fluid-saturated, poroelastic layered half-space. Earthquake Science, 26(2): 107-116. DOI: 10.1007/s11589-013-0011-6
    Jianwen Liang, Ji Zhang, Zhenning Ba. 2012: Amplification of in-plane seismic ground motion by group cavities in layered half-space (Ⅱ): with saturated poroelastic soil layers. Earthquake Science, 25(4): 287-298. DOI: 10.1007/s11589-012-0854-2
    Gengxin Yu, Liyun Fu. 2011: Iterative convergence of boundary-volume integral equation method. Earthquake Science, 24(5): 391-400. DOI: 10.1007/s11589-011-0801-7
    Haiming Zhang, Xiaoping Rui, Wenbo Zhang. 2010: Boundary integral equations for dynamic rupture propagation on vertical complex fault system in half-space: Theory. Earthquake Science, 23(2): 177-190. DOI: 10.1007/s11589-010-0083-5
    Jianwen Liang, Hao Luo, Vincent W Lee. 2010: Diffraction of plane SH waves by a semi-circular cavity in half-space. Earthquake Science, 23(1): 5-12. DOI: 10.1007/s11589-009-0084-4
    Jianwen Liang, Zhongxian Liu. 2009: Diffraction of plane P waves by a canyon of arbitrary shape in poroelastic half-space (Ⅱ): Numerical results and discussion. Earthquake Science, 22(3): 223-230. DOI: 10.1007/s11589-009-0223-y
    Jianwen Liang, Zhongxian Liu. 2009: Diffraction of plane P waves by a canyon of arbitrary shape in poroelastic half-space (Ⅰ): Formulation. Earthquake Science, 22(3): 215-222. DOI: 10.1007/s11589-009-0215-y

Catalog

    Corresponding author: Jianwen Liang, liang@tju.edu.cn

    • Department of Civil Engineering, Tianjin University, Tianjin 300072, China

    1. On this Site
    2. On Google Scholar
    3. On PubMed

    Figures(14)  /  Tables(1)

    Get Citation
    PDF
    XML
    Article views (395) PDF downloads (2) Cited by()
    Turn off MathJax
    Article Contents
    Abstract
    1.   Introduction
    2.   Formulation
    3.   Numerical implementation
    4.   Accuracy verification
    5.   Numerical results and discussion
    6.   Conclusions
    Acknowledgements
    References
    Related Articles

    震球期刊

    EQS

    E-mail Alert RSS

    Supported by: Beijing Renhe Information Technology Co., Ltd.  Baidu Analytics

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return