Download：
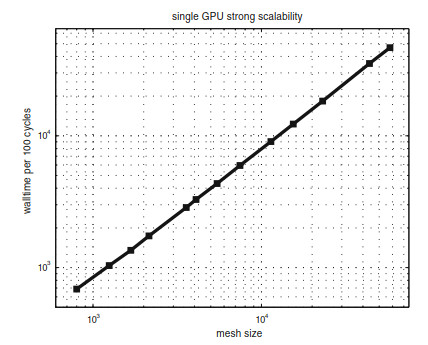
Strong scalability of our single GPU code with different mesh sizes. The black squares show the average wall-time per 100 time steps, and the number of elements varies from 800 to 57, 920
Figures of the Article
-
![]()
The flowcharts of the major steps in the reference parallel CPU codes (left) and those in our CPU-GPU hybrid implementation (right). The whole calculation can be separated into three sections: pre-processing, time-stepping, and post-processing. The pre-processing section reads and calculates all the data that the time-stepping section will use. The time-stepping section updates the DOFs of each tetrahedral element according to Eqs. (8)-(10) and has been ported to the GPU. The post-processing section is in charge of writing out the DOFs and/or the seismograms at the pre-specified locations
-
![]()
a The flowchart of the calculations in step (2), the volume contributions. "dudt" is the volume contribution, "Kxi, " "Keta, " "Kzeta" correspond to the stiffness matrices, Klkζ, Klkη, Klkζ, in the text. "JacobianDet" is the determinant of the Jacobian |J|. "nElem" is the number of tetrahedral elements in the subdomain, "nDegFr" is the number of DOFs per component per tetrahedral element, "nVar" is the number of components in the governing equation. "AStar, " "BStar, " "CStar" correspond to A*, B*, C* in the text. Code segments for the calculations in the dark-gray box are listed in b and c. b. Baseline implementation of the CUDA kernel for the "left-multiplication" between the time-integrated DOF and the stiffness matrix Klkζ. "Kxi_dense" corresponds to the dense matrix representation of Klkζ, "dgwork" corresponds to the time-integrated DOF, and the result of the multiplication is stored in "temp_DOF." c A segment of the optimized CUDA kernel for the "left-multiplication" between the time-integrated DOF and the stiffness matrix Klkζ. "Kxi_sparse" corresponds to the sparse matrix representation of Klkζ. Meanings of other symbols are identical to those in Fig. b
-
![]()
Single-GPU speedup factors obtained using 7 different meshes and 4 different CPU core numbers. The total number of tetrahedral elements in the 7 meshes is 3, 799, 6, 899, 12, 547, 15, 764, 21, 121, 24, 606, and 29, 335, respectively. The speedup factors were obtained by running the same calculation using our CPU-GPU hybrid code with 1 GPU and using the serial/parallel "SeisSol" CPU code on 1/2/4/8 CPU cores on the same compute node. The black columns represent the speedup of the CPU-GPU hybrid code relative to 1 CPU core, the dark-gray columns represent the speedup relative to 2 CPU cores, the light gray column represents the speedup relative to 4 CPU cores and the lightest gray columns represent the speedup relative to 8 CPU cores
-
![]()
Strong scalability of our single GPU code with different mesh sizes. The black squares show the average wall-time per 100 time steps, and the number of elements varies from 800 to 57, 920
-
![]()
a A perspective view of the 3D geometry of the discretized salt body in the SEG/EAGE salt model. b A two-dimensional cross-section view of the SEG/EAGE salt model along the A-A′ profile (Aminzadeh et al. 1997). The material properties for the different geological structures are listed in Table 1
-
![]()
Speedup factors of our parallel GPU codes obtained using two different mesh sizes. The number of tetrahedral elements used in our experiments are 327, 866, 935, 870. The speed factors were computed for our single-precision multiple-GPUs code with respect to the CPU code running on 16/32/48/64 cores runs on different nodes
-
![]()
Strong scalability of our multiple-GPUs codes with 1.92 million elements, the black line shows the average wall-time per 100 time steps for this size-fixed problem performed by 32-64 GPUs
-
![]()
Weak scalability of our multiple-GPUs code performed by 2-80 GPUs, the black line shows the average wall-time per 100 time steps for these size-varied problems. The average number of elements per GPU is around 53, 000 with about 6% fluctuation
-
![]()
a A perspective view of the 3D Marmousi2 model with dimension of 3, 500 m in depth, 17, 000 m in length, and 7, 000 m in width. There are 379, 039 tetrahedral elements, and each element has its own material property. There are 337 receivers locate at 5 m beneath the surface along the A-A′ (yellow) line, and the horizontal interval is 50 m; the explosive source located at 10.0 m(depth), 7, 500.0 m(length), 3, 500.0 m(width). (b). The plot of the marmousi2 model shot gather, computed by our multiple-GPUs code. Our CUDA code uses 16 GPUs spend 4, 812.64(s) calculat e 5 s seismogram, while the SeisSol runs on 16 CPU cores need 135, 278.50(s), it's a speedup of 28.11×. (Color figure online)
-
![]()
a A perspective view of the simplified SEG/EAGE salt model with dimension of 4, 200 m in depth, 13, 500 m in length and 13, 500 m in width. There are 447, 624 tetrahedral elements and each element has its own material property. There are 192 receivers locate at 5 m beneath the surface along A-A′ line and the horizontal interval is 50 m, the explosive source located at 10.0 m (depth), 7, 060.0 m (length), 4, 740.0 m (width). b The plot of the SEG/EAGE salt model shot gather, computed by our multiple-GPUs code. Our CUDA code uses 16 GPUs spend 7, 938.56(s) calculate 7 s seismogram, while the SeisSol runs on 16 CPU cores need 224, 589.80(s), it's a speedup of 28.29×
Related articles
-
2024, 37(1): 91-91. DOI: 10.1016/j.eqs.2023.12.002
-
2023, 36(3): 254-281. DOI: 10.1016/j.eqs.2023.04.002
-
2019, 32(5-6): 187-196. DOI: 10.29382/eqs-2019-0187-01
-
2018, 31(4): 75-75. DOI: 10.29382/eqs-2018-0224-6
-
2015, 28(3): 163-174. DOI: 10.1007/s11589-015-0121-4
-
2014, 27(5): 553-565. DOI: 10.1007/s11589-014-0094-8
-
2014, 27(2): 179-187. DOI: 10.1007/s11589-014-0069-9
-
2014, 27(1): 117-125. DOI: 10.1007/s11589-014-0063-2
-
2014, 27(1): 101-106. DOI: 10.1007/s11589-014-0065-0
-
2013, 26(5): 283-291. DOI: 10.1007/s11589-013-0016-1
