Identifying the occurrence time of an impending major earthquake: a review

1.   Introduction

It has been found that unique dynamic features hidden behind the time series of complex systems can be unveiled, if we analyze them in terms of natural time χ (Varotsos et al. 2001, 2002a, b). For a time series comprising N events, we define an index for the occurrence of the k-th event by χ_k = k/N, which we term natural time. We, then, study the evolution of the pair (χ_k, p_k) by using the normalized power spectrum.

defined by

where ω stands for the angular frequency, and p_k = is the normalized energy for the k-th event of energy Q_k. In the time series analysis using natural time, the behavior of Π(ω) at ω close to zero is studied for capturing the dynamic evolution, because all the moments of the distribution of the p_k can be estimated from Φ(ω) at ω→0 (see p. 499 of Feller 1971). For this purpose, a quantity κ₁ is defined from the Taylor expansion Π(ω) = 1 - κ₁ω² + κ₂ω⁴ +…, where.

The entropy S in natural time is defined as the derivative with respect to q of the fluctuation function at q = 1, which results in:

where It is dynamic entropy, and its value upon considering the time reversal T, i.e., Tp_k = p_N-k+1, is labeled by S_. The value of S_ is, in general, different from S (e.g., see Varotsos et al. 2007, 2008b, and references therein), and thus S does satisfy the conditions to be "causal." The entropy S_u of a "uniform" (u) distribution is S_u = 0.0966.

It has been found that the aforementioned quantity κ₁, the variance of natural time χ_k, is a key parameter that enables recognition of the complex dynamic system under study entering the critical stage (Varotsos et al. 2001, 2002a, b, 2011c). This occurs when the variance κ₁ converges to 0.070, as it will be discussed in detail in "Appendix". In short, Varotsos et al.(2011b, c) showed that κ₁ becomes equal to 0.070 at the critical state for a variety of dynamical models including the 2D Ising model and the self-organized criticality (SOC) Bak-Tang-Wiesenfeld sandpile model. Further, in Table 8.1 of Varotsos et al.(2011c) one can find a compilation of 14 cases in which the condition κ₁ = 0.070 has been ascertained.

Seismicity is a typical example of complex time series, and earthquakes exhibit complex correlations in time, space and magnitude (M) which have been studied by several authors (for example see Huang 2008, 2011; Lennartz et al. 2008, 2011; Rundle et al. 2012, 2016). The observed earthquake scaling laws (e.g., Turcotte 1997) indicate the existence of phenomena closely associated with the proximity of the system to a critical point (e.g., Holliday et al. 2006; Varotsos et al. 2011c). Taking this view that earthquakes are critical phenomena, an order parameter for seismicity has been introduced (Varotsos et al. 2005) by means of natural time analysis, which is just the aforementioned variance κ₁ of natural time. In this case, Q_k, and hence p_k, for earthquakes is estimated by means of the relation Q_k∝10^1.5M_k (Kanamori 1978) where M_k stands for the magnitude of the k-th earthquake.

Critical phenomena are considered, in general, of crucial importance in statistical physics in view of their applications in a multitude of diverse fields. The order parameter of a system in the critical state is expected to undergo non-Gaussian fluctuations, but almost nothing is known (Botet 2011) about the mathematical form of the possible probability distributions of the order parameter except of a few cases (Botet 2011; Carretero-Campos et al. 2012); thus, any result on the fluctuations of the order parameter is of chief importance.

Focusing on the fluctuations of the order parameter of seismicity, recent investigations based on natural time analysis revealed that they exhibit characteristic changes well before the occurrence of a major earthquake (Sarlis et al. 2010; Varotsos et al. 2012a, b, 2013). In particular, Varotsos et al. (2013) found that these fluctuations minimize when a series of low-frequency (≤0.1 Hz) electric signals (Uyeda et al. 2002, 2009), termed Seismic Electric Signals (SES) activity, initiates (cf. these signals are generated when the gradually increasing stress in the preparation area of an impending earthquake reaches a critical value, e.g., see Varotsos et al. 1993). In addition, beyond this simultaneous appearance of two different geophysical observables (SES activity and seismicity), Varotsos et al. (2013) showed that these two phenomena are also linked closely in space, which opened the window for a reliable estimation of the epicentral area of an impending major earthquake. This has been subsequently confirmed by Sarlis et al. (2015) for all major mainshocks of magnitude 7.6 or larger that occurred in Japan during 1984-2011 by applying a procedure that will be shortly described later in Sect. 4. Independent experiments in Greece (Varotsos and Lazaridou 1991; Varotsos et al. 1993) as well as in other earthquake prone areas (for a review, see Varotsos et al.2011c; Lazaridou-Varotsos 2013) have shown that an SES activity has a lead time of the order of a few months.

The challenging issue discussed here is to review—considering the aforementioned recent advances—the current knowledge as far as the narrowing of the time window of an impending major earthquake from a few months to around 1 week or so. Along these lines, we present in Sects. 2 and 3 the description of the identification procedure for the occurrence time of an impending major earthquake when geoelectrical data are either available or lacking, respectively. A brief discussion follows in Sect. 4, and finally in Sect. 5 we summarize our conclusions in the light of the recent advances based on natural time analysis. The physical basis of the condition κ₁ = 0.070 that identifies the approach to the critical point (the mainshock in this dynamic phase-change is the new phase) is discussed in "Appendix".

2.   Identifying the occurrence time of a major earthquake when geoelectrical data are available

The relation for the critical state that has been explicitly shown to be valid for SES activities (Varotsos et al. 2001, 2011c):

for ω→0, simplifies to

which shows that the second-order Taylor expansion coefficient of Π(ω), i.e., κ₁, is equal to 0.070. This was also shown to be valid for earthquake models, e.g., for the time series of avalanches in the "train" Burridge-Knopoff earthquake model as well as in the Olami-Feder-Christensen earthquake model (see pp. 345-348 and 349-363 in Varotsos et al.(2011c), respectively), when the system approaches the critical point.

Once a SES activity has been recorded, the candidate epicentral area to suffer the mainshock can be estimated on the basis of the so-called selectivity map of the station at which the SES was recorded and in addition by considering the ratio of the two SES components (e.g., Varotsos and Lazaridou 1991; Varotsos et al. 1993). Thus, we find in principle some area, labeled hereafter A. As for the magnitude M of the expected earthquake, it is estimated through the relation log₁₀ (∆V/L) ≈ 0.3 M + const. (e.g., see Varotsos and Lazaridou 1991) for a given measuring dipole of length L and a given seismic area, where the SES amplitude ∆V/L is found from the anomalous variation ∆V of the potential difference between the two electrodes of the dipole.

To determine the occurrence time of the impending mainshock, we start the natural time of seismicity in the candidate area immediately after the SES initiation since it signals when the system enters the critical stage. Two procedures have been suggested:

A procedure, which for the sake of convenience is called preliminary procedure, was used during the period 2001-2008 (e.g., see Varotsos et al. 2001, 2005, 2006b, c, 2008b; Varotsos 2005). Since there has been, however, some room for subjective judgment to identify the approach to critical stage, because the time variation of parameters was traced only on a single subarea, a more objective procedure, which for reasons of brevity is called "updated" procedure, has been developed by Sarlis et al. (2008) that considers the natural time analysis of the seismicity in all the possible subareas, instead of a single area, of the area A. More details on these two procedures are now given below.

2.1   The preliminary procedure to determine the occurrence time of the impending mainshock

We set the natural time zero at the initiation time of the SES activity, as mentioned, and then form time series of seismic events in natural time for the area A, each time when a small EQ above a magnitude threshold M ≥ M_thres occurs and in other words, when the number of the events increases by one. The normalized power spectrum in natural time Π(ω) for ω→0 (or the variance κ₁) for each of the time series is computed for the pairs (χ_k, Q_k) or (χ_k, p_k) and compared with that of Eq. (5) for ω ∈ [0, π]. We also calculate the evolution of the quantities S and S_ to ascertain that the condition S, S_ < S_u (see p. 292 of Varotsos et al. 2011c) is also satisfied. The actual criteria for recognizing a true coincidence of the observed time series with that of critical state were as follows (Varotsos et al. 2001, 2006c, b, 2008b, 2011c; Varotsos 2005; Uyeda et al. 2009):

First, the "average" distance between the curves of Π(ω) of the evolving seismicity and Eq. (5) should be smaller than 10^-2 (cf. this was regarded as showing that = 0). This is a practical criterion for stopping calculation.

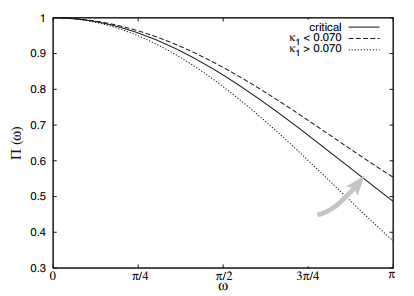
Second, the final approach of the evolving Π(ω) to that of Eq. (5) must be by descending from below as shown by the gray arrow in Fig. 1. This alternatively means that before major EQs, the κ₁ value gradually changes with time and finally approaches from above that of the critical state, i.e., κ₁ = 0.070.

Figure  1.  Schematic diagram showing the behavior of Π(ω) in natural time for ω ∈ [0, π]. Solid line is Π(ω) resulting from Eq. (5) for critical stage (κ₁ = 0.070), whereas two other lines are for κ₁ > 0.070 and κ₁ < 0.070. The gray arrow indicates how the Π(ω) curve approaches the critical one from below

DownLoad: Full-Size Img PowerPoint

Third, both values S and S_ should be smaller than S_u at the coincidence.

Finally and fourth, since the process concerned is supposed to be self-similar (critical dynamics), the time of the occurrence of the true coincidence should not vary, in principle, upon changing (within reasonable limits) the magnitude threshold M_thres and the size of area A.

We clarify that if higher magnitude threshold is used, the description of the real situation approaching criticality is expected to become less accurate due to "coarse graining" (Varotsos 2006; Varotsos et al. 2006a) when the number of events is finite. On the other hand, the description becomes more accurate when using a lower magnitude threshold since a larger number of events is involved into the calculation. The following point is worthwhile to be mentioned here. It has been found by Varotsos et al. (2005) that at least six earthquakes are needed for obtaining reliable κ₁ value. In other words, the use of high magnitude thresholds leading to a number of earthquakes smaller than six is not recommended for obtaining reliable κ₁ value and hence for a description of the real situation approaching criticality.

It has been observed (Varotsos et al. 2001, 2006c, b, 2008b; Varotsos 2005) that the aforementioned true coincidence appears usually a few days (up to around one week) before the occurrence of the mainshock.

2.2   The updated procedure to determine the occurrence time of the impending mainshock

The basic idea behind this approach suggested by Sarlis et al. (2008) is the following: When area A reaches criticality, one expects in general that all its subareas have also reached criticality simultaneously. At that time, therefore, the evolution of seismicity in each of these subareas is expected to result in κ₁ value close to 0.070. Assuming equipartition of probability among the subareas, the distribution Prob(κ₁) of the κ₁ values of all subareas should be peaked at around 0.070 exhibiting also magnitude threshold invariance [cf. more details on the selection of subareas can be found in Sarlis et al. (2008) or in p. 300 of Varotsos et al. (2011c)]. This usually occurs a few days to around 1 week before the mainshock; thus, it enables the prediction of the occurrence time of major EQs with time window of the order of a week or less.

2.3   Application to the major M_W6.9 earthquake that occurred in southwestern Greece on 14 February 2008

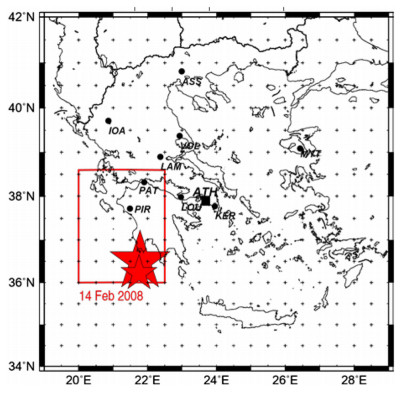
An SES activity was recorded (see Fig. 2b) on 14 January 2008 at the station PIR of the VAN telemetric network (Fig. 3) operating in Greece (Varotsos et al. 2008a). Furthermore, a longer duration SES activity of the same polarity and amplitude was recorded also at PIR (depicted in Fig. 7.17(c) of Varotsos et al. 2011c) almost one week later. The SES amplitude revealed that the expected earthquake magnitude exceeded the threshold to issue a prediction (cf. in Greece only when expected M is 6.0 or larger, a prediction is publicized). Thus, a prediction was publicized on 1 February 2008 by Varotsos et al. (2008a) in the www.arXiv.org database of the library of Cornell university.

Figure  2.  The SES activities recorded on 10 January 2008 at PAT (a) and on 14 January 2008 at PIR (b) in normalized units (i.e., by subtracting the mean value and dividing the results by the standard deviation) along with the dichotomous representation depicted by the dotted (blue) line. Taken from Varotsos et al. (2008a)

DownLoad: Full-Size Img PowerPoint

Figure  3.  The computation for the determination of the occurrence time for the M_W6.9 EQ on 14 February 2008 (large red star) was made by considering the seismicity within the red rectangle N_36.0^38.6 E_20.0^22.5, which was the expected epicentral area (Varotsos et al. 2008a). Solid dots show the stations of the VAN telemetric network

DownLoad: Full-Size Img PowerPoint

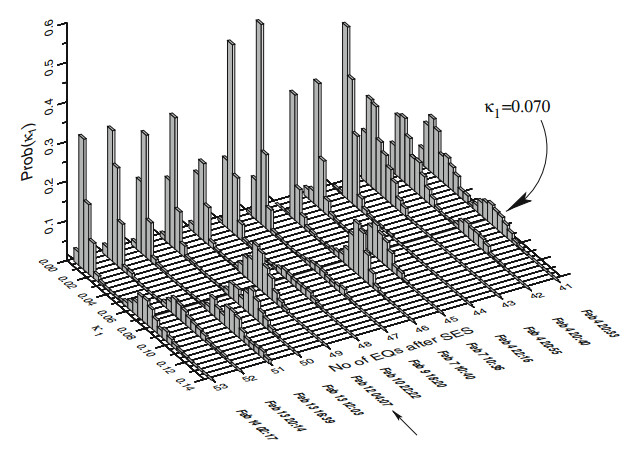
The study of the seismicity in natural time was immediately started in the area A:N_36.0^38.6 E_20.0^22.5 (which had been determined on the basis of SES properties by means of the procedure described above) as publicized on 1 February 2008 by Varotsos et al. (2008a). This area is marked with the red line in Fig. 3. We now mention a difficulty arisen if the preliminary procedure is applied to the present case. Within this area N_36.0^38.6 E_20.0^22.5 studied since the initiation of the SES activity on 14 January 2008, two EQs with magnitudes M_L ≈ 5.0 occurred on 4 February 2008 close to PAT station (see Fig. 3) associated with an SES activity recorded at PAT on 10 January 2008, see Fig. 2a. This results in the fact that the computed κ₁ value becomes very small, i.e., κ₁ ≈ 0, at any small area surrounding the epicenters of these two EQs (see Varotsos et al. 2005). On the other hand, in the updated procedure the computation of κ₁ is extended to all possible subareas of the area N_36.0^38.6 E_20.0^22.5. Then the probability distribution Prob(κ₁) of κ₁ (shown in Fig. 4 for M_thres = 3.2), constructed after the occurrence of each small event, exhibited a bimodal feature. The one mode, corresponding to nearly zero κ₁ values, results from the subareas that contain the aforementioned two EQs close to PAT of magnitude 5.0. The other mode, maximized at κ₁ = 0.070, comes from subareas which do not include these two EQs. It is the latter mode that upon the occurrence of a small event at 04:07 UT on 12 February 2008, see the case marked with an arrow in Fig. 4, signifies the approach to the critical point. Two days later, i.e., at 10:09 UT on 14 February 2008, the M_W6.9 earthquake occurred at 36.5°N 21.8°E inside the expected area N_36.0^38.6 E_20.0^22.5. After 2 h, i.e., at 12:08 UT, a magnitude M_W6.2 EQ followed almost at the same epicenter (see the small star in Fig. 3).

Figure  4.  Determination of the occurrence time of the major earthquake on 14 February 2008. Study of the Prob(κ₁) versus κ₁ for the seismicity (M_thres = 3.2) within the area N_36.0^38.6 E_20.0^22.5 after the SES activity at PIR on 14 January 2008 depicted in Fig. 2b

DownLoad: Full-Size Img PowerPoint

Beyond the aforementioned updated procedure, the preliminary one was simultaneously applied, but upon avoiding the difficulty described above. In particular, we excluded the influence of the aftershocks around the two M_L ≈ 5.0 earthquakes that had already occurred close to PAT on 4 February 2008. This led to the conclusion that the critical point was approached somewhat earlier, i.e., on 10 February 2008 instead of the date 12 February 2008 mentioned above (cf. the difference in the results of the two procedures can be understood on the basis of the point concerning the "coarse graining" when using different magnitude thresholds mentioned above). This explains why we were able to publicly announce on 10 February 2008 that a major earthquake of magnitude larger than 6.0 is imminent, as described in detail by Uyeda and Kamogawa(2008, 2010) and in pp. 173-179 of Lazaridou-Varotsos (2013).

By summarizing this case, we can say the following: All the parameters of the M_W6.9 earthquake that occurred on 14 February 2008, which is the strongest one in Greece since 1983, i.e., the epicentral area (see the red rectangle in Fig. 3), the magnitude and the occurrence time were specified and announced publicly in advance.

3.   Identifying the occurrence time of a major earthquake when geoelectrical data are lacking

For earthquakes of magnitude around 6.5 or larger, it has been ascertained that the magnetic field variations that accompany SES activities become clearly detectable (e.g., Varotsos et al. 2003) mainly on the z-component (Sarlis and Varotsos 2002). Thus, it is evident that when geoelectrical data are lacking but geomagnetic data are available, the initiation time of an SES activity can be identified upon recognizing the time at which the anomalous magnetic field variations start. However, in this case, we cannot follow the procedure described in Sect. 2 since the latter variations cannot provide an SES selectivity map and hence an estimate of the epicentral area of the impending major earthquake.

In case that geoelectrical data are not available, and in order to determine the initiation time of an SES activity we recall the finding of Varotsos et al. (2013) mentioned in the Introduction that this initiation occurs almost at the time at which the fluctuations of the order parameter of seismicity in a large area exhibit a minimum. In addition, we recall that a spatiotemporal study of this minimum, as also mentioned in the Introduction and briefly described in the next subsection, enables an estimate of the epicentral area of the impending major earthquake (Sarlis et al. 2015).

3.1   Application to the M_W9 Tohoku earthquake that occurred on 11 March 2011 in Japan

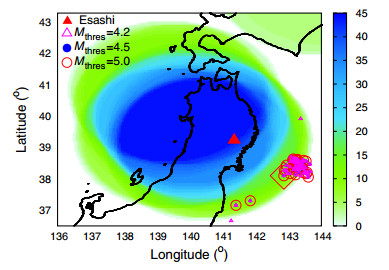
Concerning the starting time of the natural time analysis of seismicity, we choose the date of 5 January 2011 which is the date of the appearance of the minimum of the fluctuations of the order parameter of seismicity before this major earthquake reported by Sarlis et al. (2013). This, which is remarkably the deepest minimum ever observed during the period 1984-2011 investigated, almost coincides with the initiation of an SES activity—being in accordance with the findings by Varotsos et al. (2013)—since anomalous magnetic field variations appeared during the period 4-14 January 2011 on the z-component at two measuring sites (Esashi and Mizusawa) lying at epicentral distances of around 130 km (Xu et al. 2013; Han et al. 2015, 2016).

Concerning the estimation of the epicentral location of the impending mainshock without making use of SES data, we follow the procedure developed by Sarlis et al. (2015): By dividing the entire Japanese region N₂₅⁴⁶ E₁₂₅¹⁴⁸ (large area) into small areas, a calculation of the fluctuations of κ₁ of seismicity is carried out on them. Some small areas show a minimum of the fluctuations almost simultaneously with the minimum in the entire Japanese region (on 5 January 2011) and such small areas cluster within a few hundred kilometers from the actual epicenter. Such a calculation leads to an estimate of the candidate epicentral area depicted with the blue-green area in Fig. 5.

Figure  5.  Estimation of the M_W9 Tohoku earthquake epicenter. Color contours of the number of the small areas exhibiting minimum of the fluctuations of κ₁ almost simultaneous with that in the entire Japanese region. The red diamond shows the M_W9 Tohoku earthquake epicenter and the red triangle the location of Esashi measuring magnetic station (the other measuring station, Mizusawa, lies only a few tens of km far from Esashi). The epicenters of earthquakes occurring within the candidate epicentral area (blue-green) after 5 January 2011 and before the M_W9 Tohoku earthquake for various thresholds are also shown

DownLoad: Full-Size Img PowerPoint

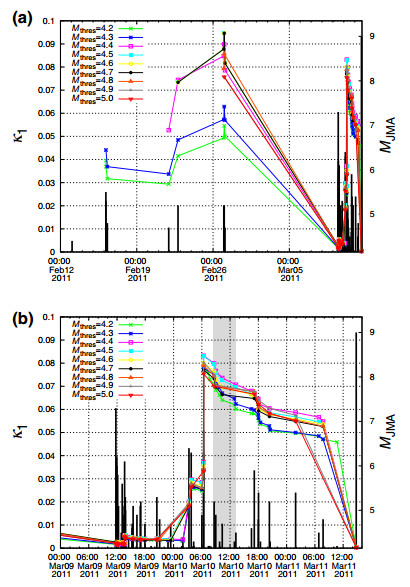
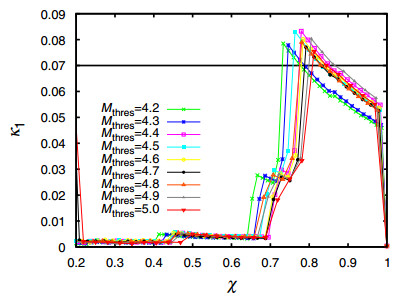
We now compute the κ₁ values of seismicity in the blue-green area by starting from 5 January 2011 (using the conversion formulae suggested by Tanaka et al. 2004, for the relation between M_JMA and M_w). The results are depicted in Fig. 6 for M_thres = 4.2-5.0. Recalling that at least six earthquakes are needed (Varotsos et al. 2005) for obtaining reliable κ₁ value, which happens in the blue-green area on 16 February 2011 for M_thres = 4.2, we depict in Fig. 6a the computed κ₁ values during the last 4 weeks before the M_W9 Tohoku earthquake occurrence. This figure clearly shows that the condition κ₁ = 0.070 is not satisfied for all magnitude thresholds at least until the M7.3 earthquake on 9 March 2011. Since the results afterward cannot be seen clearly in Fig. 6a, we plot in expanded time scale in Fig. 6b (see also Fig. 7) the κ₁ values of seismicity from 00:00 LT on 9 March 2011 until the Tohoku earthquake occurrence. This figure reveals that the condition κ₁ = 0.070 (which signals that the mainshock is going to occur within the next few days or so) is fulfilled for M_thres = 4.2-5.0 in the morning of 10 March 2011 upon the occurrence of the earthquakes from 08:36 to 13:14 LT, i.e., almost one day before the Tohoku earthquake (see the gray shaded area in Fig. 6b).

Figure  6.  Determination of the occurrence time of M_W9 Tohoku earthquake. The evolution of the κ₁ values of seismicity (left scale) in the blue-green area in Fig. 5 together with the earthquakes (right scale) shown with thick black vertical bars are plotted versus the conventional time: a Since 12 February 2011 until the M_W9 Tohoku earthquake occurrence on 11 March 2011. b Since 00:00 LT on 9 March 2011 until the Tohoku earthquake occurrence. The shaded area marks the period in the morning of 10 March 2011 during which the condition κ₁ = 0.070 is fulfilled (see the text)

DownLoad: Full-Size Img PowerPoint

Figure  7.  The evolution of the κ₁ values of seismicity in a similar fashion as in Fig. 6b, but plotted versus natural time χ (χ = 1 corresponds to the occurrence of the M_W9 Tohoku earthquake, while χ ≈ 0.2 to the M7.3 foreshock on 9 March 2011)

DownLoad: Full-Size Img PowerPoint

Thus, in short, natural time analysis of seismicity leads to the conclusion that the κ₁ values converge to 0.070 almost one day before the Tohoku earthquake occurrence, which points to the approach of the system to the critical point (mainshock) almost one day before the mainshock occurrence. It is remarkable that this approach happened after the M7.3 earthquake on 9 March 2011, thus showing that this earthquake was a foreshock.

4.   Discussion

The method we followed in order to estimate the epicentral area before the Tohoku earthquake occurrence, which has the privilege that can be applied when geoelectrical data are lacking, cannot be misinterpreted as replacing the one applied in general when using the SES properties since its accuracy is obviously worse. A direct comparison cannot be made in the present case because the SES selectivity maps of the two stations (Esashi and Mizusawa), where the anomalous magnetic field variations (characteristic of an SES activity) appeared were unknown since earlier SES data on these stations were not available.

The procedure applied here to determine the Tohoku earthquake occurrence could be viewed in the following context: Upon recalling that the minimum of the order parameter fluctuations of seismicity appears almost simultaneously with the initiation of an SES activity, the present method may be interpreted as showing that the study of the seismic events that occur just before the emission of SES activity bears enough information for a reliable estimate of the future epicentral area. In addition, the natural time analysis of the events that occur in the candidate epicentral area just after the initiation of the SES activity leads to the identification of the occurrence time of the impending mainshock. Hence, by recapitulating, we may say that natural time analysis of the seismic events that occur both just before and just after the SES emission, reveal in principle an estimate of the parameters (i.e., the epicentral area and the occurrence time, respectively) of the impending major mainshock.

It is worthwhile to notice that before using the minimum of the fluctuations of seismicity to deduce the epicentral area of the impending mainshock, it is a prerequisite to ascertain that this minimum is truly a precursory one of a major earthquake by applying the criteria that distinguish the non-precursory minima from the precursory ones as described in "Appendix" of Varotsos et al. (2014) (see also Sarlis et al. 2016).

5.   Conclusions

In the light of the recent advances achieved by means of natural time analysis of seismicity, we presented the procedures to identify the occurrence time—within a time window of a week or so—of an impending major mainshock in both cases, i.e., if geoelectrical data are available or not. In these two cases, we considered as examples the strongest earthquakes that occurred in Greece and Japan, respectively, during the period after 1984, and identified the time at which the critical point (mainshock occurrence) has been approached. In the former case, the M_W6.9 earthquake that occurred on 14 February 2008 in southwestern Greece was publicly announced as imminent almost four days in advance, i.e., on 10 February 2008. In the latter case, concerning the M_W9 Tohoku earthquake that occurred in Japan on 11 March 2011, the critical point has been approached almost one day in advance, i.e., in the morning of 10 March 2011. This is of prominent importance since natural time analysis enabled the recognition that the approach to the critical point (mainshock) happened almost a day after the occurrence of the M7.3 earthquake of 9 March 2011, thus recognizing that this M7.3 earthquake was a foreshock.

Open Access

This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Appendix: Explanation of κ₁ = 0.070 for critical systems

We start with a few introductory remarks on nonequilibrium dynamics and the scaling hypothesis (Varotsos et al.2011b,c): The approach to equilibrium, from a nonequilibrium initial state, in a system at its critical point is usually described by a scaling theory with a single growing length scale, ξ(t) ∝ t^1/z , where z is the dynamic exponent that governs the equilibrium dynamics. Such a case is called the single growth model. Thus, the physical meaning of ξ(t) is just the length scale up to which critical correlations have been established at time t.Dynamic scaling, for large t, suggests:

where z is the so-called dynamic exponent characterizing temporal correlations in equilibrium. This equation shows that relaxation to equilibrium is governed by the same exponent as correlations in equilibrium. In addition, we note that this relation holds independently of the nonequilibrium initial state, which can affect the scaling function, but not the exponent z (Bray et al. 2000).

We deal with time series of signals emitted from complex dynamical systems, i.e., systems comprising interacting components that evolve with time. In natural time analysis, when the system is in thermodynamic equilibrium, it should produce stationary time series with probabilities p_k independent of χ_k. The situation is drastically different when the system is not in equilibrium. When the system approaches the critical state, clusters of the new phase are formed by enhanced fluctuations and their size increases as does the correlation length. But this happens not instantly, because long range correlations develop gradually leading to the so-called dynamic phase transition (critical transition) (Bray 1994; Stanley 1999; Sicilia et al. 2007; Varotsos et al. 2011b, c). Thus, the time series emitted in such a nonequilibrium process will be nonstationary and p_k, or the corresponding probability density function p(χ) will no longer be independent of χ.

By using for p(χ) the expression

the normalized power spectrum of Π(ω), see Eq (1), can be written as

A Taylor expansion of this equation around ω→0 leads to

Since p(χ) is the normalized energy released at χ, for a dynamical system at criticality, it also characterizes the way energy is released during the evolution of the dynamic transition. Energy release may be caused by some existing external field coupled with the newly forming phase (Varotsos et al. 2011b, c). The interaction energy density may comprise several terms the most significant of which is usually expected to be of the dipole type; for example, the interaction Hamiltonian density h_int = - E·p (h_int = - B·m) in the case of an electric E (magnetic B) external field, where p (m) stands for the electric (magnetic) dipole moment density of the new phase. This interaction energy density is proportional to the linear dimension of the newly forming phase (the system volume is kept constant), and hence, it is proportional to the correlation length ξ (cf. this has been explicitly shown in pp. 364-365 of Varotsos et al. 2011c). According to the dynamic scaling hypothesis (see Bray (1994); Sicilia et al. (2007) and references therein), the time-dependent correlation length ξ at dynamic phase transitions scales as ξ ∝ t^1/z, where z is as mentioned above the so-called dynamic critical exponent. The time t is usually measured in Monte Carlo steps. Assuming that the dynamic scaling hypothesis should also hold for p(χ) at criticality, we expect (Varotsos et al.2011b,c):

where ζ is another dynamic exponent, and N_c a normalization factor to make In fact, this equation is plausible from the definition of p_k, i.e., it represents the normalized energy emitted during the k-th event and the energy at criticality has a power law distribution. By inserting Eq (11) into Eq (10), we obtain:

Substituting the value of ζ by the dynamic critical exponent z for various universality classes of critical systems tabulated by Odor (2004), we can obtain the corresponding values of κ₁. Since for most universality classes z varies in a region from z = 2 to z = 2.4, we find that the values of κ₁ obtained are in the range 0.068-0.071. In particular for the two-dimensional (2D) Ising model, one has z = 2.165 (Ito 1993) leading through Eq. (12) to κ₁ = 0.0697 ≈ 0.070 if we assume z = ζ. These results seem to justify the substitution of ζ by z, strongly suggesting that they are the same dynamic exponent. This is not unreasonable since, in reality, the Monte Carlo steps used in the computation of z actually correspond to natural time steps.

In the mean field case, e.g., the growing centrally fed sandpile model suggested by Wiesenfeld et al. (1990), which is a deterministic version of the original Bak-Tang-Wiesenfeld SOC model, we have ζ = 2 (see pp. 368-371 of Varotsos et al. 2011c). By inserting this value into Eq. (12), we find that the corresponding κ₁ value is κ₁ = 0.0686. This value is very close to the value κ₁ ≈ 0.070.