We discuss two array-based tomography methods, ambient noise tomography (ANT) and two-planewave earthquake tomography (TPWT), which are capable of taking advantage of emerging large-scale broadband seismic arrays to generate high resolution phase velocity maps, but in complementary period band: ANT at 8–40 s and TPWT at 25–100 s period. Combining these two methods generates surface wave dispersion maps from 8 to 100 s periods, which can be used to construct a 3D vS model from the surface to ~200 km depth. As an illustration, we apply the two methods to the USArray/Transportable Array. We process seismic noise data from over 1 500 stations obtained from 2005 through 2009 to produce Rayleigh wave phase velocity maps from 8 to 40 s period, and also perform TPWT using ~450 teleseismic earthquakes to obtain phase velocity maps between 25 and 100 s period. Combining dispersion maps from ANT and TPWT, we construct a 3D vS model from the surface to a depth of 160 km in the western and central USA. These surface wave tomography methods can also be applied to other rapidly growing seismic networks such as those in China.
In recent years, large-scale arrays of broadband seismographs have been emerging across different continents, such as the EarthScope USArray in the USA, the China Digital Seismic Network, F-net in Japan, etc. These dense, large scale arrays provide the opportunity to image subsurface seismic structures at unprecedented resolution. The development of large scale seismic instrumentation also requires the improvements in tomography methodology to achieve the potential that these arrays offer. High resolution models of subsurface structures at large scales promise to advance the knowledge of tectonics and geodynamic processes across continents.
Ambient noise tomography is typically performed at periods shorter than ~40 s, which mainly provides constraints on the structure of crust and uppermost mantle. To provide constraints on deeper structures and more completely image the structures of the lithosphere and asthenosphere, long period surface waves (> 50 s) are required. Long period surface waves may also be obtained from ambient noise tomography (e.g., Bensen et al., 2008, 2009; Nishida et al., 2009), but this probably requires very long baselines between stations. Alternatively, long period surface waves can be extracted from large teleseismic earthquakes, which usually excite long period surface waves that propagate over thousands of kilometers. New array-based tomography methods such as those developed by Yang and Forsyth(2006a, b), Pollitz (2008), and others produce dispersion maps with resolutions similar to ambient noise tomography. Our method is built on the method of Yang and Forsyth (2006a), called two-plane-wave tomography (TPWT), which uses the interference of two plane-waves to model each incoming teleseismic wavefield. This method was originally developed to image regional scale structures with an aperture typically less than 1000 km. For a continental-scale array with a scale of thousands of kilometers, we have generalized the method by dividing a large area to an arbitrary number of sub-regions and fitting each incoming wavefield at each sub-region with two plane waves (e.g., Yang et al., 2008). The current paper is an update of the study of Yang et al. (2008).
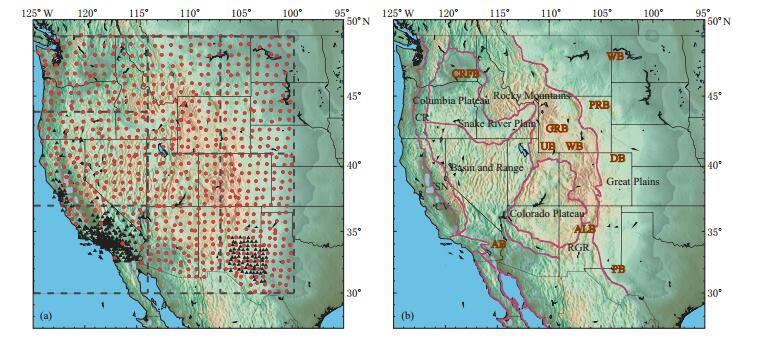
Combining the two array-based tomography methods, ambient noise tomography and two-plane-wave tomography, we are able to image structures at high resolution from the surface to ~200 km depth. In this paper, we discuss the two methods and also demonstrate their application to the large-scale Transportable Array (TA) of EarthScope/USArray (Figure 1). We present Rayleigh wave phase velocity maps constructed by ANT at periods of 8–40 s and TPWT at periods of 25–100 s using ambient noise and teleseismic earthquake data, respectively, from the TA and several other regional arrays in the western US in 2005–2009. In addition, we present the inversion for 3D vS structures by combining the resulting Rayleigh wave phase velocity dispersion maps from ANT and TPWT and briefly discuss the resulting 3D model.
Figure
1.
(a) Station coverage in the western US. The EarthScope USArray Transportable Array is plotted as circles, and regional arrays CI, BK and XP are plotted as triangles. The division of the sub-regions for twoplane-wave tomography is outlined with dashed lines. (b) Major geological units in the western US are outlined and identified with names and abbreviations: Rocky Mountains, Columbia Plateau, Cascade Range (CR), Snake River Plain, Basin and Range, Sierra Nevada Mountains (SN), Central Valley (CV), Colorado Plateau, and Rio Grande Rift (RGR). Major sedimentary basins are indicated with orange-red abbreviations (from north to south): Williston Basin (WB), Columbia River sub-Flood Basalt sediment (CRFB), Powder River Basin (PRB), Green River Basin (GRB), Uinta Basin (UB), Washakie Basin (WB), Denver Basin (DB), Central Valley (CV), Albuquerque Basin (ALB in New Mexico), Altar Basin (AB in southern California), Permian Basin (PB).
We process continuous vertical component ambient noise data from 2005 to 2009 recorded by ~1 500 stations including the TA, the US National Seismic Network (US), and several regional arrays (Figure 1). The average inter-station distance is around 70 km. The Transportable Array is a network of 400 high-quality broadband seismographs that have been emplaced in temporary sites since 2004 across the conterminous United States from west to east in a regular grid pattern with station spacings of about ~70 km. Each instrument is deployed at one place for about two years and then removed and re-deployed to the next carefully selected location on the eastern edge of the array. So far, instruments have been deployed in more than 1 000 locations.
The ambient noise data processing procedure applied here is similar to that described in detail by Bensen et al. (2007) and Lin et al. (2008). Continuous data are decimated to one sample per second and then filtered in the period band from 5 to 100 s. Instrument responses are removed from the continuous data because different types of seismic sensors are used among the stations. Because the amplitudes of ambient noise at ~6–8 s period dominate the spectra, spectral whitening is applied to flatten spectra over the entire period band (5–100 s). Time-domain normalization is then applied to suppress the influence of earthquake signals and other irregularities. After these processes are completed, cross-correlations are performed daily and then are stacked over five years between 2005 and 2009. Then, an automated frequency time analysis (FTAN) is used to measure the dispersion curves of the Rayleigh waves. Careful attention is paid to data selection based on signal-to-noise ratio (SNR), inter-station distances and data consistency.
Surface wave tomography is applied on the selected dispersion measurements to produce Rayleigh wave phase speed maps on a 0.5°by 0.5°grid using the ray theoretic method of Barmin et al. (2001). Both damping and smoothing are applied in the tomography. The choice of damping and smoothing parameters is based on the optimization of data misfit and model smoothness and determined after a series of tests using various values. Finally, the resulting Rayleigh wave dispersion maps are constructed between of 8 and 40 s period with a typical resolution within the array of ~50 km.
2.2
Two-plane-wave tomography (TPWT)
The measurement of the dispersion characteristics of teleseismic surface waves crossing a regional array of seismometers is a powerful means to detect variations in lithospheric and asthenospheric structures. However, a crucial question is how to represent the incoming wavefield accurately. A conventional approach is to regard incoming waves as plane waves propagating along greatcircle paths and then to measure the phase differences between station pairs aligned along the same path. Amplitude and waveform variations are commonly observed across a seismic array, particularly at shorter periods, and indicate scattering or multi-pathing caused by lateral heterogeneities between the earthquake and the array. These effects can distort the incoming waves, causing deviations in azimuth and leading to wavefield complexity. Neglect of the non-planar character of the incoming wavefield can systematically bias the measured phase velocities (Wielandt, 1993).
In the two-plane-wave tomography method, an incoming teleseismic wavefield is modelled using the interference of two plane-waves, each with initially unknown amplitude, initial phase, and propagation direction (Forsyth et al., 1998; Forsyth and Li, 2005), yielding a total of six parameters that describe the incoming wavefield for each teleseismic event. Finite frequency effects (e.g., Dahlen et al., 2000; Zhou et al., 2004) are also considered in this method because the goal is to resolve structures with scales the order of a wavelength. This two-plane-wave representation has been successfully applied to regional arrays in several continents to obtain phase velocities (Li et al., 2003; Weeraratne et al., 2003; Yang and Forsyth, 2006a, b ).
In the context of a large-scale array like the TA (Figure 1), the size of the region of study is larger than the limit of the two-plane-wave assumption. Thus, we partition the western US into seven sub-regions with 2° overlaps in both latitude and longitude. The seven subregions are shown in Figure 1a. As a result, each of the regions has a scale less than 1 000 km, in which an incoming teleseismic wavefield can be modeled quite well with two plane-waves. The two-plane-wave tomography is performed separately in each of these seven subregions using a 0.5°×0.5°grid. The final phase velocity maps across the whole western USA are constructed by including phase velocities from all of the individual sub-regions and averaging phase velocities in the areas of overlap.
In data processing, about 450 teleseismic events that occurred from 2005 to 2009 (Figure 2) with MS > 5.5 and epicentral distances from 30°to 150°relative to the center of the array are selected. These events together with the large number of stations generate highly dense ray coverage, which allows us to produce high-resolution phase velocity maps. After all the event data are collected, the instrument responses, means and trends of seismograms are removed and then the vertical components of Rayleigh waves are filtered with a series of narrow-bandpass (10 mHz), four-pole, double-pass Butterworth filters centered at frequencies ranging from 10 to 40 MHz (25–100 s). Fundamental mode Rayleigh waves are isolated from other seismic phases by cutting the filtered seismograms using boxcar time windows with a 50 s half cosine taper at each end. The width of the boxcar window is determined according to the width of the fundamental mode Rayleigh wave packet. The filtered and windowed seismograms are converted to the frequency domain to obtain amplitude and phase measurements. Details of the data processing procedure are described by Yang and Forsyth(2006a, b).
Figure
2.
Azimuthal equidistant projection of earthquakes used for two-plane-wave tomography. This plot is centered at (104°W, 35°N) (triangle). The straight lines connecting each event to the center (triangle) are great-circle paths.
The resulting phase velocity maps from ANT and TPWT are plotted in Figures 3 and 4, respectively. At 8 s period, in the short period end of ANT, Rayleigh wave phase velocity is most sensitive to shear velocities at depths shallower than ~10 km. Low velocities are imaged in all of the major sedimentary basins as indicated in Figure 1. At intermediate periods of ANT (16 s and 24 s), Rayleigh wave phase velocities mainly reflect the shear velocities in the middle and lower crust. Low velocities associated with sedimentary basins diminish at these periods. Four major low velocity anomalies are observed: in Yellowstone, the eastern edge of the Basin and Range, the Rocky Mountains, and the western fringe of the Colorado Plateau. High velocity anomalies are observed beneath the Columbia River Flood Basalts and in the southern Basin and Range.
Figure
3.
Phase velocity maps from ambient noise tomography with reference velocity (vref) 3.05, 3.25, 3.55 km/s at periods (T) of 8, 16 and 24 s.
At periods longer than 50 s (Figure 4), surface waves are mainly sensitive to shear velocities in the uppermost mantle. At these periods, low velocities are observed in the Columbia Plateau, the Basin and Range, the Snake River Plain and near the western, eastern and southern edges of the Colorado Plateau. A strong velocity contrast exists between the tectonically active western US and the cratonic central US in these maps.
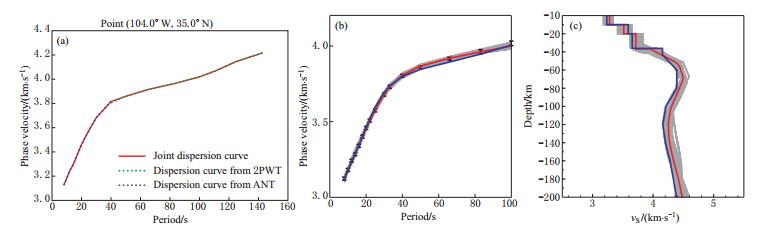
In the overlapped period band between the two tomographic methods, from 25 s to 40 s, phase velocities from these methods are quite similar. For example, Figure 5 plots the phase velocity maps from ANT and TPWT at 40 s period and their difference. The RMS of the difference between these two maps is about 1%. Agreement is very good in most areas with a difference less than 0.5%. The differences of phase velocities from these two methods are quite similar at other overlapped periods. Differences are more pronounced, however, near the boundaries of the sub-regions divided in TWPT where edge effects apparently are significant (e.g., Idaho, the western edge of Utah, middle Colorado and southern New Mexico) and near the fringes of the array where resolution is lower, particularly near the eastern edge of northern and southern Dakota, Nebraska, and Kansas. Thus, in order to reduce the edge effects in the two-plane-wave tomography, we plan in the future to improve the two-plane-wave tomography by performing tomography simultaneously over all subregions with an integrated grid. Some differences in phase velocities could also arise from the different wave propagation theories assumed in the two tomography methods. In ANT, ray theory is assumed because periods of Rayleigh waves used in ANT are shorter than 40 s and finite frequency effects are insignificant for surface waves at these periods. However, in TPWT, we employ Born sensitivity kernels (Zhou et al., 2004) to account for finite frequency effects because we use surface waves at periods up to 100 s.
Figure
5.
Phase velocity maps at 40 s from ANT (a) and TPWT (b) as well as the velocity difference between ANT and TPWT at 40 s (c).
By combining results from the full set of tomographic maps, we can construct a 3D isotropic shear velocity model. Because only Rayleigh waves are used in the inversion and they are primarily sensitivity to vSV, the resulting model is in fact a vSV model but will be referred to as vS hereafter. At each geographic point of the 0.5°×0.5°grid, a local Rayleigh wave phase speed curve is extracted from the dispersion maps at periods from 8 to 100 s and this curve provides the data for the vS inversion. The inversion is performed using a two-step procedure. This two-step procedure has been used and thoroughly discussed in previous studies (e.g., Bensen et al., 2009; Yang et al., 2008) and we only briefly describe it here.
The first step is a linearized inversion of the Rayleigh wave phase velocity curve for the best fitting vS-model below each grid point. In the linearized inversion, depth-dependent shear wave velocities are parameterized in eleven constant vS layers from the Earth's surface to 200 km depth with three layers for the crust and eight layers for the upper mantle. The model parameters are slightly damped and smoothed vertically. Because Rayleigh wave phase speeds depend primarily on vS, we scale vP to vS using a constant vP/vS ratio of 1.735 in the crust and 1.756 in the mantle (Chulick and Mooney, 2002). Due to the trade-off between Moho depth and vS in the layers directly above and below the Moho, in this first step, we fix crustal thickness to that derived from receiver functions (Gilbert and Fouch, 2007).
In the second step, a Markov Chain Monte-Carlo resampling of model space is performed to quantify the uncertainty in shear velocity versus depth (Shapiro and Ritzwoller, 2002). The Markov Chain Monte-Carlo inversion executes a random walk through model space starting from the model derived from the linearized inversion. At each spatial node, this generates an ensemble of "acceptable" local 1D shear velocity models that fit the Rayleigh wave dispersion curve within specified uncertainties. In this step, depth-dependent shear wave speeds are parameterized by three crustal layers and five B-spline functions in the upper mantle to represent mantle velocity to a depth of 200 km, rather than by eight layers in the upper mantle in the linearized inversion. If the predicted dispersion curve for a candidate model from Markov Chain Monte-Carlo resampling matches the measured curve with an average misfit of less than twice the dispersion measurement uncertainties, the model is retained and termed "acceptable".
An example of the two-step procedure at one location is plotted in Figure 6. For each grid point, the average of the resulting ensemble of acceptable models at each depth is taken as the expected value of the vS model and the half-width of the corridor of the ensemble provides an estimate of model uncertainty (Figure 6c). By assembling the individual vS model profiles for each grid point, we form the 3D model. Here, we present four vS maps at depths of 5, 15, 60 and 120 km (Figure 7) and briefly describe the major velocity features imaged.
Figure
6.
An example of vSV inversion for the point at (104°W, 35°N). (a) The observed dispersion curve from ambient noise tomography (blue) and from TPWT (green). (b) The observed dispersion curve (same as the red line in Figure 6a) is shown with error bars at individual periods. The blue line is the predicted dispersion curve from the vSV model of the linear inversion. Gray lines are predicted dispersion curves from the ensemble of vSV models from the Monte-Carlo inversion shown in Figure 6c. The red line is the predicted dispersion curve from the average of the ensemble of vSV models. (c) The vSV models (gray lines) and the average of the ensemble (red line) from the Monte-Carlo inversion. The blue line is the vSV model from the linear inversion.
Figure
7.vSV maps at depths (h) of 5, 15, 60, and 120 km, plotted as perturbations relative to the average velocity shown in the lower-left corner of each panel.
In the upper crust, most significant velocity features are low velocities in the major sedimentary basins, including the Central Valley of California, and the Uinta, Green River, Washakie, Powder River, Denver, Albuquerque, Permian, Anadarko and Williston Basins. In contrast, high velocities are observed for the mountain ranges, including the Sierra Nevada, the Peninsular Range, and the central and southern Rocky Mountains and also in the Colorado Plateau. In the whole crust, low velocities are observed throughout the Basin and Range province and the Columbia River Flood Basalt province probably due to elevated crustal temperatures resulting from relatively thin lithosphere and young magmatism and extension (Zandt et al., 1995).
In the uppermost mantle, the most striking feature is the transition from overall low velocities observed in the western US to overall high velocities observed in central US. This lateral west-to-east transition is clearly correlated with the western Rocky Mountain front, the boundary between the tectonically active western US and the stable and cratonic eastern US. Other than the high velocities in the cratonic central US, moderate high velocities are observed in the northern and central Colorado Plateau and in the central Rocky Mountains in the area of northern Idaho and western Montana, which implies that the Proterozoic lithosphere in these areas may still be present and not completely eroded by past tectonic events such as the Laramide Orogeny. On the contrary, seismic velocities become quite low in the southern Rocky Mountain, implying Proterozoic lithosphere may be altered or removed. Prominent low velocities are observed throughout the Basin and Range province and the Columbia River Flood Basalt province and along the Snake River Plain and the Rio Grand Rift. The low velocities in the Columbia River Flood Basalt province and along the Snake River Plain are probably related to the Yellowstone and Newberry hotspot tracks, following the impact of the mantle plume head beneath the lithosphere that occurred near the boundary of Oregon and Nevada at ~16.6 Ma (Camp and Ross, 2004; Xue and Allen, 2007). Low velocities underlying the Basin and Range province may reflect lithospheric thinning consistent with the buoyant upwelling of asthenospheric material in response to the detachment of the Farallon plate in the post-Laramide era from ~50 to 20 Ma (Humphreys et al., 2003). Low velocities are also observed at the edges of the Colorado Plateau except on the northern side, indicating large parts of the Proterozoic lithosphere beneath the Colorado Plateau have been eroded.
4.
Summary
In this paper, we discuss two array-based tomography methods, ambient noise tomography and two-plane-wave earthquake tomography. Ambient noise tomography is based on cross-correlations of ambient seismic noise data to obtain short-period surface wave dispersion maps, which provide constraints on the structure of crust and uppermost mantle. Two-plane-wave tomography is a method to generate intermediate- and long-period surface wave dispersion maps using teleseismic earthquake data, which provide constraints on upper mantle structure. In this method, each teleseismic wavefield is modelled as the interference of two incoming plane waves, each with initially unknown amplitude, initial phase and propagating direction. By combining these two complementary methods, we can generate surface wave dispersion maps from ~8 s to ~100 s, which enables us to construct 3D shear velocity model from surface to ~200 km depth.
For illustration, we apply these two methods to the recent deployment of USArray/Transportable Array, covering the western and central US so far. We present Rayleigh wave phase velocity maps constructed by ambient noise tomography at periods of 8–40 s and two-plane-wave tomography (TPWT) at periods of 25– 100 s using ambient noise and teleseismic earthquake data from TA and several other regional arrays in western US in 2005–2009. In addition, we present the inversion for 3D vS structure by combining the resulting Rayleigh wave phase velocity dispersion maps from ANT and TPWT and briefly discuss the resulting 3D model.
These surface wave tomography methods have also been applied to the rapidly growing seismic instrumentations in China (e.g., Yang et al., 2010) but mostly at regional scales and generated numerous regional models. In the near future, with the extension of coverage over the whole China, these methods can be adopted to construct a high resolution continental-scale 3D model over the whole China just as across the continental USA.
Acknowledgements
We would like to thank Prof. Fenglin Niu for encouraging the submission of this paper. We also thank two anonymous reviewers for their constructive comments to improve the manuscript. Instruments (data) used in this study were made available through EarthScope (www.earthscope.org), supported by the US National Science Foundation (EAR-0323309). The facilities of the IRIS Data Management System, and specifically the IRIS Data Management Center were used for access to the waveform and metadata required in this study. This work has been supported by NSF under grants EAR-0711526 and EAR-0844097 and also by Macquarie University CORES start-up grant to Y. Yang. This is contribution 701 from the Australian Research Council National Key Centre for the Geochemical Evolution and Metallogeny of Continents (http://www.gemoc.mq.edu.au).
Arroucau P, Rawlinson N and Sambridge M (2010). New insight into Cainozoic sedimentary basins and Palaeozoic suture zones in southeast Australia from ambient noise surface wave tomography. Geophys Res Lett37: L07303.
Barmin M P, Ritzwoller M H and Levshin A L (2001). A fast and reliable method for surface wave tomography. Pure Appl Geophys158(8): 1 351-1 375. doi: 10.1007/PL00001225
Behr Y, Townend J, Bannister S and Savage M K (2010). Shear velocity structure of the Northland Peninsula, New Zealand, inferred from ambient noise correlations. J Geophys Res115: B05309.
Bensen G D, Ritzwoller M H, Barmin M P, Levshin A L, Lin F, Moschetti M P, Shapiro N M and Yang Y (2007). Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophys J Int169: 1 239-1 260. doi: 10.1111/gji.2007.169.issue-3
Bensen G D, Ritzwoller M H and Yang Y (2009). A 3-D shear velocity model of the crust and uppermost mantle beneath the United States from ambient seismic noise. Geophys J Int177: 1 177-1 196. doi: 10.1111/gji.2009.177.issue-3
Bensen G D, Ritzwoller M H and Shapiro N M (2008). Broadband ambient noise surface wave tomography across the United States. J Geophys Res113(B5): B05306, doi: 10.1029/2007JB005248.
Camp V E and Ross M E (2004). Mantle dynamics and genesis of mafic magmatism in the intermontane Pacific Northwest. J Geophys Res109: B08204, doi: 10.1029/2003JB002838.
Cho K H, Herrmann R B, Ammon C J and Lee K (2007). Imaging the upper crust of the Korean Peninsula by surface-wave tomography. Bull Seismol Soc Am97: 198-207. doi: 10.1785/0120060096
Chulick G S and Mooney W D (2002). Seismic structure of the crust and uppermost mantle of North America and adjacent oceanic basins: A synthesis. Bull Seismol Soc Am92(6): 2 478-2 492, doi: 10.1785/0120010188.
Dahlen F A, Hung S -H and Nolet G (2000). Frechet kernels for finite frequency travel times Ⅰ. Theory. Geophys J Int141: 157-174. doi: 10.1046/j.1365-246X.2000.00070.x
Fang L H, Wu J P, Ding Z F and Panza G F (2010). High resolution Rayleigh wave group velocity tomography in North China from ambient seismic noise. Geophys J Int181(2): 1 171-1 182.
Forsyth D W and Li A (2005). Array-analysis of twodimensional variations in surface wave phase velocity and azimuthal anisotropy in the presence of multipathing interference. In: Levander A and Nolet G eds. Seismic Earth: Array Analysis of Broadband Seismograms. Geo physical Monograph 157, AGU, Washington DC, 81-98.
Forsyth D W, Webb S, Dorman L and Shen Y (1998). Phase velocities of Rayleigh waves in the MELT experiment on the East Pacific Rise. Science280: 1 235-1 238. doi: 10.1126/science.280.5367.1235
Gilbert H and Fouch M J (2007). Complex upper mantle seismic structure across the southern Colorado Plateau/Basin and Range Ⅱ: Results from receiver function analysis. Eos Trans AGU88(52), Fall Meet Suppl, Abstract S41B-0558.
Humphreys E, Hessler E, Dueker K, Erslev E, Farmer G L and Atwater T (2003). How Laramide-age hydration of North America by the Farallon slab controlled subsequent activity in the western U. S. In: Klemperer S L and Ernst W G eds. The George A. Thompson Volume: The Lithosphere of Western North America and Its Geophysical Characterization. Int. Book Ser, vol. 7, Geol Soc of Am, Boulder, Colo, 524-544.
Kang T S and Shin J S (2006). Surface-wave tomography from ambient seismic noise of accelerograph networks in southern Korea. Geophys Res Lett33(17): L17303. doi: 10.1029/2006GL027044
Li A, Forsyth D W and Fischer K M (2003). Shear velocity structure and azimuthal anisotropy beneath eastern North American from Rayleigh wave inversion. J Geophys Res108(B8): 2 362, doi: 10.1029/2002JB002259.
Li H Y, Su W, Wang C Y and Huang Z X (2009). Ambient noise Rayleigh wave tomography in western Sichuan and eastern Tibet. Earth Planet Sci Lett282(1-4): 201-211. doi: 10.1016/j.epsl.2009.03.021
Liang C and Langston C A (2009). Three-dimensional crustal structure of eastern North America extracted from ambient noise. J Geophys Res114: B03310, doi: 10.1029/2008JB005919.
Lin F C, Moschetti M P and Ritzwoller M H (2008). Surface wave tomography of the western United States from ambient seismic noise: Rayleigh and Love wave phase velocity maps. Geophys J Int173: 281-298. doi: 10.1111/gji.2008.173.issue-1
Lin F C, Ritzwoller M H, Townend J, Bannister S and Savage M K (2007). Ambient noise Rayleigh wave tomography of New Zealand. Geophys J Int170: 649-666. doi: 10.1111/gji.2007.170.issue-2
Moschetti M P, Ritzwoller M H and Shapiro N M (2007). Surface wave tomography of the western United States from ambient seismic noise: Rayleigh wave group velocity maps. Geochem Geophys Geosys8: Q08010, doi: 10.1029/2007GC001655.
Nishida K, Montagner J P and Kawakatsu H (2009). Global surface wave tomography using seismic hum. Science326(5949): 112. doi: 10.1126/science.1176389
Pollitz F F (2008). Observations and interpretation of fundamental mode Rayleigh wavefields recorded by the Transportable Array (USArray). Geophys J Int173: 189-204. doi: 10.1111/gji.2008.173.issue-1
Saygin E and Kennett B L N (2010). Ambient seismic noise tomography of Australian continent. Tectonophysics481: 116-125. doi: 10.1016/j.tecto.2008.11.013
Shapiro N M, Campillo M, Stehly L and Ritzwoller M H (2005). High-resolution surfacewave tomography from ambient seismic noise. Science307: 1 615-1 618. doi: 10.1126/science.1108339
Shapiro N M and Ritzwoller M H (2002). Monte-Carlo inversion for a global shear velocity model of the crust and upper mantle. Geophys J Int151: 88-105. doi: 10.1046/j.1365-246X.2002.01742.x
Villaseñor A, Yang Y, Ritzwoller M H and Gallart J (2007). Ambient noise surface wave tomography of the Iberian Peninsula: Implications for shallow seismic structure. Geophys Res Lett34: L11304, doi: 10.1029/2007GL030164.
Weeraratne D S, Forsyth D W, Fischer K M and Nyblade A A (2003). Evidence for an upper mantle plume beneath the Tanzanian craton from Rayleigh wave tomography. J Geophys Res108(B9), doi: 10.1029/2002JB002273.
Wielandt E (1993). Propagation and structural interpretation of non-plane waves. Geophys J Int113: 45-53. doi: 10.1111/gji.1993.113.issue-1
Xue M and Allen R M (2007). The fate of the Juan de Fuca plate: Implications for a Yellowstone plume head. Earth Planet Sci Lett264: 266-276, doi: 10.1016/j.epsl.2007.09.047.
Yang Y and Forsyth D W (2006a). Regional tomographic inversion of the amplitude and phase of Rayleigh waves with 2-D sensitivity kernels. Geophys J Int166: 1 148-1 160. doi: 10.1111/gji.2006.166.issue-3
Yang Y and Forsyth D W (2006b). Rayleigh wave phase velocities small-scale convection and azimuthal anisotropy beneath southern California. J Geophys Res111: B07306, doi: 10.1029/2005JB004180.
Yang Y, Zheng Y, Chen J, Zhou S, Savas C, Sandvol E, Tilmann F, Priestley K, Hearn T M, Ni J F, Brown L D and Ritzwoller M H (2010). Rayleigh wave phase velocity maps of Tibet and the surrounding regions from ambient seismic noise tomography. Geochem Geophys Geosys11(8): Q08010, doi: 10.1029/2010GC003119.
Yang Y, Ritzwoller M H, Lin F C, Moschetti M P and Shapiro N M (2008). Structure of the crust and uppermost mantle beneath the western United States revealed by ambient noise and earthquake tomography. J Geophys Res113: B12310. doi: 10.1029/2008JB005833
Yang Y J, Ritzwoller M H, Levshin A L and Shapiro N M (2007). Ambient noise Rayleigh wave tomography across Europe. Geophys J Int168(1): 259-274. doi: 10.1111/gji.2007.168.issue-1
Yao H J, Beghein C and van der Hilst R D (2008). Surface wave array tomography in SE Tibet from ambient seismic noise and two-station analysis-Ⅱ. Crustal and uppermantle structure. Geophys J Int173(1): 205-219. doi: 10.1111/gji.2008.173.issue-1
Yao H J, van der Hilst R D and de Hoop M V (2006). Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis-Ⅰ. Phase velocity maps. Geophys J Int166(2): 732-744. doi: 10.1111/gji.2006.166.issue-2
Zandt G, Myers S C and Wallace T C (1995). Crust and mantle structure across the Basin and Range-Colorado Plateau boundary at 37°N latitude and implications for Cenozoic extensional mechanism. J Geophys Res100: 10 529-10 548, doi: 10.1029/94JB03063.
Zhou Y, Dahlen F A and Nolet G (2004). Three-dimensional sensitivity kernels for surface wave observables. Geophys J Int158: 142-168, doi: 10.1111/j.1365-246X.2004.02324.x.
DownLoad:
