The dilatancy-diffusion hypothesis, earthquake prediction, and operational earthquake forecasting: In memory of Professor Amos Nur on the 50^th Anniversary of the 1975 Haicheng Earthquake

1.   Introduction

The dilatancy-diffusion hypothesis (Nur, 1972; Anderson and Whitcomb, 1973; Scholz et al., 1973; Aggarwal et al., 1973; Whitcomb et al., 1973;) states that as an earthquake is approaching, stress increase would first cause dilatancy, i.e., the opening of microcracks in the vicinity of the impending earthquake. Because the rapidly opened microcracks would be dry, there would be a decrease of pore pressure and consequently the reduction of seismic P-wave velocity. As fluid diffusion into the microcracks subsequently occurred, the fluid pressure would recover and the seismic velocity would increase to its initial value and reduce the shear strength of the faults, this process eventually triggers the occurrence of the earthquake.

The dilatancy-diffusion hypothesis has served as the major theoretical pillar for the existence of earthquake precursors and the justification of the tempt of earthquake prediction. In a much broader sense, dilatation is materials’ volume increase due to deformation. The dilatancy-diffusion hypothesis was applied to a few smaller earthquakes in Central Asian and the New York State (Aggarwal et al., 1973) but caused little attention to the scientific community. The encouraging outcome of the ‘prediction’ of the 1975 Haicheng Earthquake (Adams, 1976; National Research Council, 1976; Wang KL et al., 2006) marks the triumph of the dilatancy-diffusion hypothesis and generated optimistic enthusiasm among scientists all over the world. Unfortunately, merely one year later, with a dramatic turning, the tragic 1976 Tangshan Earthquake claimed loss hundreds of thousands of lives and formed one of the most catastrophic losses in the 20^th century (Blume, 1980). Prior to the main event, a very tortuous, debatable and unfortunately, failed ‘prediction’ practice marked the insufficiency and ineffectuality of the dilatancy-diffusion hypothesis for earthquake prediction (Mei SR, 1986). This event brought a prolonged ‘quiet and cold’ view of this theory and a deep reflection of the broader realm of ‘earthquake prediction’ for the entire geophysical community in the world.

The dilatancy-diffusion hypothesis interpreted the physical phenomena observed prior to some earthquakes, including seismic velocity variations, groundwater ups and downs, electric resistivity changes, gas emissions and so on. As the major theoretical hypothesis that can reasonably interpret earthquake precursors it certainly bears the scientific competence to deserve more systematic examination.

At the time of the 50^th anniversary of the 1975 Haicheng Earthquake, it is the right time to thoroughly review the development of the dilatancy-diffusion hypothesis and its role in earthquake prediction. It is also the right time to review the contribution of the dilatancy-diffusion hypothesis to earthquake precursor studied spearheaded by Professor Amos Nur (1938−2024). A detailed scrutiny of the dilatancy-diffusion hypothesis will benefit the research of seismology in the next several decades, to assist seismologists to tackle earthquake prediction, or more preferably, earthquake forecasting, an ultimate need from society.

I will develop my argument in the sequence of the following sections. In section 2, I will first briefly summarize the origin of the dilatancy theory in the geotechnical engineering world that mainly dealt with the mechanics of granular materials. Then I will expand the discussion for the major development into dilatancy of rocks, that may contain cracks and fractures. However, most of the physical experiments are carried out on intact rock samples. In Section 3, I focus on the development of the dilatancy-diffusion hypothesis and its application to interpret earthquake precursors and guide the earthquake prediction practice. I will amplify Prof. Nure’s contribution to the dilatancy-diffusion hypothesis in this section. As a matter of fact, most of the reported anomalous precursors cannot stand up to independent scrutiny. In Section 4 I discuss the reason of why there is only limited success in earthquake prediction by applying the dilatancy-diffusion hypothesis and pointing out the reason as the non-linearity and uncertainty of upscaling of the results from the laboratory experiments to the Earth’s crust. For the road ahead, the whole earthquake seismology community has realized we have to shift from deterministic prediction to statistic forecasting for dealing with pending earthquake risk. Thus, in Section 5 I will first discuss the concept of operational earthquake forecasting (OEF). Next, I will discuss the role of deep learning in OEF with an emphasis on the implementation of the physically-informed neural network (PINN) and discuss a couple of encouraging PINN application cases. Finally, in Section 6 I conclude the whole paper by restating the major points and arguments developed in previous sections. Finding the best way to reduce earthquake loss is the obligated social responsibility of the seismological research community.

2.   Laboratory experiments on dilatancy prior to failure

2.1   A brief recount of the development of the dilatancy theory in geotechnical engineering

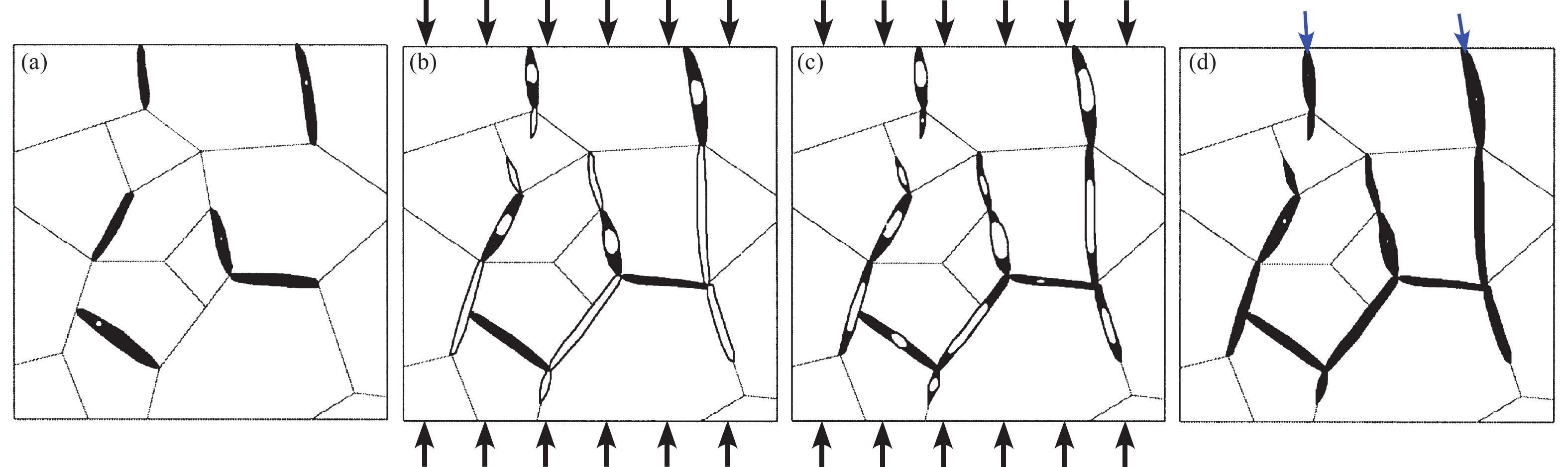
The dilatancy theory originated in the field of geotechnical engineering for granular material studies. The primary goal of the theory is to explain the volumetric behavior of soils and other granular materials under shear stress. Reynolds (1885) considered the first to describe the phenomenon of dilatancy in the late 19th century. Reynolds observed that densely packed granular materials, such as sand, exhibit an increase in volume (dilatancy) when subjected to shear deformation. He demonstrated this effect through laboratory experiments. The key principle of dilatancy theory is that the volume of granular material depends on its particle arrangement. Under shear load dense, materials tend to dilate (expand in volume) because particles need to move apart to allow sliding. Meanwhile, loose materials tend to contract. This behavior is now referred to as Reynolds dilatancy (Figure 1).

Figure  1.  (a) Left-lateral shear occurred on all layers of a group of close-packed cylinders. Contact gap portion increase can be seen from all layers, a representation of 2-dimensinal dilatancy; (b) concentrated shear occurred on a single layer of a group of densely-packed cylinders. Contact gap increase (dilatancy) occurred only on the single fracture. (modified from Mead, 1925).

DownLoad: Full-Size Img PowerPoint

Reiner (1945) developed the mathematical expression of the phenomenon of dilatancy without taking into account the internal structure of the material. He showed that on purely mathematical grounds dilatancy can be viewed as one constitutive relation for a generalized Newtonian liquid. Reiner’s (1945) work laid the theoretical foundation for expanding the dilatancy theory to deal with more material types other than granular material.

In the mid-20th century, the dilatancy theory was refined and formalized by researchers such as Karl Terzaghi and later Rowe (1954), who applied it to soil mechanics and geotechnical engineering. Terzaghi (known as ‘the father of soil mechanics’) introduced effective stress principles and related the dilatancy behavior to shear strength.

Rowe advanced the theory further in the 1960s by introducing the stress-dilatancy relationship (Rowe, 1962), linking the rate of volumetric strain to the rate of shear strain. He noticed the difference of the orientation of the angles of friction and dilatation. This finding was independently verified later by others (e.g., Bolton, 1986; Houlsby, 1991). This was particularly useful for predicting soil behavior in triaxial and plane strain tests.

Granular material mechanical response is largely dominated by the evolution of dilatancy, fabric and void ratio histories. To account for this fact, Wan RG and Guo PJ (1999) outlined a mathematical description of the stress dilatancy behavior of granular materials particularly accounted for stress level and void ratio dependencies. The consideration of these aspects has important implications in the modeling of granular material behavior. The starting point in their study is the well-established Rowe's theory which was revisited and ultimately modified by introducing a factor linked to governing state parameters to describe the complete behavior of granular materials during deformation. Numerical simulations of triaxial tests on granular materials at different void ratios and stress levels were presented to illustrate the model.

After coming into the new millennium, engineers and scientists in geomechanics keep being enthusiastic about the dilatancy theory for granular materials. A few examples are presented below.

Yin ZY and Chang CS (2013) conducted a set of laboratory experiments with two types of sand. Their experimental results have shown quite different stress-dilatancy behavior for sand under loading and unloading conditions. The experimental results have also shown significant effects of inherent anisotropy. Using a micromechanics-based method they obtained the stress-dilatancy relation through the consideration of slips at the interparticle contacts in all orientations. Their experiments showed that at the end of loading stage, different planes mobilized to different shear to normal stress ratios. Subsequently, at the beginning of unloading, the local dilatancy rate at different planes starts from different values but with the same negative slope. For the loading test, the contact planes 18° and 28° behave only on contraction; other planes mobilize to a higher stress level and reach the dilation region. For the unloading test, the contact planes 55° and 72° behave only on contraction and other planes behave on contraction followed by dilation.

Yin and Chang’s results also show that for densely packed sand, the apparent interparticle friction angle is greater than the internal friction angle (Yin ZY and Chang CS, 2013). When the packing structure dilates, the degree of interlocking and the apparent frictional angle are reduced, which results in a strain-softening phenomenon. For loose packing, the apparent frictional angle is smaller than the internal friction angle. These findings are a modern confirmation of previous results (Bolton, 1986; Houlsby, 1991). Using discrete element modeling simulation technique, Ferdowsi et al. (2013) studied the phenomenon of microslips as the precursors of large slip events. They found that the emergence of microslips and their duration are controlled by the value of the slipping contact ratio and are therefore related to the jamming/unjamming transition of frictional granular packings.

Rahimi (2019) attempted to summarize plastic potential and specially stress-dilatancy relations so far proposed for constitutive modeling of cohesionless and cemented sands. Stress-dilatancy relation is usually not the same under compression and extension conditions. Furthermore, it may also be different under loading and unloading conditions. Therefore, the focus of his paper is mainly on the proposed stress-dilatancy relations for compressive monotonic loading. Moreover, because the plastic potential function can be calculated by integration of the stress-dilatancy relationship, more weight is allocated to the stress-dilatancy relationship in this research. Meanwhile, Das et al. (2019) proposed a scaling theory that links the amount of dilation as a function of shear rate and the dissipative parameters of the granular assembly.

Rocks display plastic behavior when the loads exceed their elastic limit. Naturally, the phenomena of dilatancy were also found in lithified materials like rocks. The similarity in deformation features between granular materials and rocks stimulated laboratory experiments on rock dilatancy. Dilatancy in lithified materials (fractured rocks) is the theme of the next section.

2.2   Experimental results of dilatancy in rocks at laboratory scale

Dilatancy refers to the phenomenon where a rock experiences an inelastic volume increase due to the development of microscopic cracks or the opening of existing pore spaces when subjected to stress load. For saturated rocks pore water will eventually flow in and fill the newly opened cracks, this is diffusion, clearly under a drained condition.

Mead (1925) should be considered the first to broaden the dilatancy theory to geological materials beyond granular materials (Frank, 1965). He indicated that ‘the factors controlling the manner of deformation of unconsolidated granular’ can be ‘applied by analogy to a consideration of the manner of deformation by fracture and by rock flowage’.

Using several different rock-types, Edmond and Paterson (1972) observed dilatancy persists well into the ductile (plastic) field. In some cases, notably sandstone, compaction can be followed by dilation as straining continues. Their results showed that the stress-strain curves are significantly affected by the occurrence of volume changes because of the work done through them by the confining pressure.

Using Westerly granite rock samples Zoback and Byerlee (1975) investigated the effect of microcrack dilatancy on the permeability. They emphasized the study of the relationship between permeability and volumetric strain under constant confining pressure and pore pressure as a function of increasing and decreasing differential stress. Permeability was found to increase appreciably during dilatancy. Also, (1) permeability and dilatant volume changes are not unique functions of differential stress; (2) permeability changes with differential stress are not uniquely dependent upon dilatant volume changes. The most significant implication of these findings is that if dilatancy-fluid diffusion occurs in situ, microcrack dilatancy is not a reasonable physical mechanism to account for such a phenomenon. Other reasons must be sought to explain these complications. Using analytic tools Nikolaevsky et al. (1991) derived a formulation of the mathematical dilatancy theory and conditions at strong discontinuities.

In contrast to the crystalline igneous rocks, intact rock salt has exceptionally low permeability and high ductility and is an ideal host rock for storage caverns. Rock salt deforms plastically without the formation of dilating cracks when stress remains within the non-dilatant stress domain. Schulze et al. (2001) presented experiment results on the transport properties of rock salt for the transition from non-dilatant to dilatant deformation under the condition of the dilatancy boundary. When loading up into the dilatant stress domain, damage (the porosity enhancement) and permeability are controlled by several parameters but the most important ones are the minimum principal stress and loading geometry, while pore pressure affects only the mechanical properties of the damaged and dilated rock salt.

Stanchits et al. (2003) presented laboratory experiments to observe variations of P-wave velocity and attenuation during loading process till failure with pore pressure maintained on a cylindrical sample of Westerly granite. Their results clearly demonstrated the dilatancy-diffusion process as illustrated with Figure 2 (modified from their Figure 14). It is noteworthy to point out that the dilatancy-diffusion process has passed the poroelastic deformation (Wang HF, 2000) phase and entered the inelastic deformation realm.

Figure  2.  Idealized sequence of crack growth and re-saturation corresponding to the temporal process of the dilatancy-diffusion model. Shaded cracks are liquid filled; unshaded portions of cracks are vapor filled. (a) Randomly oriented pre-existing cracks are fully saturated. (b) Following stress load (black arrows) increases, new (dry) cracks open, and favorably oriented existing cracks dilate and become partially saturated. (c) Before recharge from external pore fluid system can re-saturate cracks, local redistribution of pore water occurs to wet crack surfaces and minimize vapor bubble surface area. With time, this process tends to eliminate small bubbles and leads to the partial recovery of P-wave velocity. (d) Eventually, diffusion of water (blue arrows) from outside the dilatant zone results in re-saturation of all pores, recovery of pore fluid pressure, and further increase in P-wave velocity (based on Figure 14 of Stanchits et al., 2003 with modification).

DownLoad: Full-Size Img PowerPoint

Walton and Diederichs (2015) proposed a new model for the dilation of brittle rocks based on laboratory compression test data with separate treatment of dilatancy mobilization and decay. The feature of their model is high flexibility to accommodate a broad range of data, from various levels of data quality to distinct types of rocks.

Dilatancy is understood as inelastic volume changes of rock under conditions of differential stress not only foreshadows brittle rock failure, preceding such phenomena as earthquakes or mining-induced rock bursts, but also defines the kinematics of rock deformation. Cieślik (2018) studied the relation of dilatancy and rock stiffness changes and showed that there is a quantitative relationship between the dilatancy occurring at different levels of rock load and the development of fracturing that accompanies the process of rock degradation. Based on the mechanical laboratory test results of a fine-grained sandstone, Cieślik (2018) presented analyses of plastic volume changes in rock samples and a certain measure of fracture development accompanying the process of their degradation. Based on the characteristics obtained through mechanical tests with unloading, the inelastic volumetric strain of the samples can be established, and the scalar damage variable continuum damage mechanics (CDM) approach can be determined at various load levels. These results demonstrated the relationship between dilatancy and rock stiffness changes describing the development of fracturing. Three load intervals were determined, in which the nature of the analyzed phenomena, i.e. dilatancy and damage describing the development of cracks, undergoes significant changes. The highest intensity of both phenomena was obtained in the post-critical load range, between the ultimate strength limit and the residual strength of the samples, in which rock samples undergo the process of degradation the most.

Zhang SP et al. (2024) studied slip velocity-dependent dilatation. In this study, they combined displacement- and velocity-dependent aperture models to reproduce the transient shear-induced dilatancy of fractures in sandstone in 16 normal stress unloading tests. Their results show that the combined aperture model can describe the transient fracture aperture evolution during accelerating slip induced by normal stress unloading better than the model dependent only on slip displacement. Slip velocity could enhance the aperture increase on smoother fractures at lower normal stresses and higher slip velocities. Both the dilation factor and characteristic slip distance decrease with increasing normal stress and surface roughness, signifying reduced contribution of slip velocity to transient shear-induced dilatancy at higher normal stresses and surface roughness. The dilation angle increases with the increase of surface roughness, and this increase diminishes at higher normal stresses primarily attributable to more severe asperity wear.

Besides studying the above more classic topics, recent development in dilatancy theory for rock materials focuses on its refinement to address complexities in rock mechanics. From the author’s personal point of view the key advancements may be listed as below:

1) Noncoaxial or multi-axial behavior for rock materials: Research integrates noncoaxial effects (misalignment between stress and deformation (strain rate) due to the anisotropic property of rocks) into dilatancy models using property-dependent plastic potential theory. This provides more accurate predictions of deformation in anisotropic Earth materials under stress.

Typical laboratory testing protocol commonly involves increasing the axial stress σ₁ vertically on a cylindrical specimen at constant strain rate under fixed axisymmetric confining pressure (σ₂=σ₃) exerted by a hydraulic fluid. Any dilatancy can be accommodated readily by a reduction in fluid volume to maintain the confining pressure constant. In contrast, dilatancy in nature is typically accompanied by an increase in the confining stresses because of boundary condition given by the surrounding solid rocks. During the test the mean stress and the breaking shear stress both increase in time, corresponding to load-strengthening behavior. In nature σ₂ and σ₃ are neither fixed nor equal in the general case.

To conform with the general reality of the stress state in the crust, more recent experiments with modern apparatus were developed from pseudo-triaxial to true triaxial (Haimson and Chang C, 2000; Chang CD and Haimson, 2012; Ma XD and Haimson, 2016; Ma XD et al., 2017). The main feature of the new true-triaxial cell is very high loading capability in all three orthogonal directions, enabling testing to failure of hard crystalline rocks subjected to large least and intermediate principal stresses. All three principal stresses applied to rectangular prismatic specimens are servo-controlled. The cell was used to conduct an extensive series of tests in Westerly Granite (Haimson and Chang C, 2000) and sandstones (Ma XD and Haimson, 2016). By including the effect of the intermediate principal stress σ₂ turns out to be so significant that it raises serious questions about the suitability of rock failure criteria such as those named after Mohr, Coulomb, Griffith (1921), and others. Measurements of strain in all three principal directions revealed that the onset of dilatancy relative to the major principal stress at failure rises substantially as the intermediate principal stress increases. The true triaxial tests also demonstrate that for the same least horizontal stress σ₃ the main fracture dip angle in Westerly granite increases as a function of the intermediate principal stress σ₂, suggesting a strengthening effect (Haimson and Chang C, 2000). Limited thin section and scanning electron microscope study shows that microcrack propagation, crack localization, and main fracture characteristics are basically like those observed in conventional triaxial tests. Taking advantage of the true-triaxial cell and the confirmation of the bifurcation theory to relate the stress conditions at failure to the development of failure planes (Ma XD et al., 2017), it is ready to tie bifurcation in rock failure with shear-wave birefringence (also known as shear-wave splitting) in geophysics (Crampin et al., 1984; Gao Y and Crampin, 2008), mutually due to the alignment of microcracks.

Tsegaye (2021) carried out a new stress-dilatancy relation tuned towards the modelling of deformation behavior of rocks and rock masses. The formulation is established in both plane strain and full 3D and accommodates both loading and unloading in shear, also including the effect of possible non-coaxiality between eigen directions of plastic strain increments and stresses.

2) Dynamic loading on non-uniform multi-phase rock samples. Laboratory tests typically utilize intact uniform samples of rock to produce as uniform a stress field as possible under controlled conditions. This introduces a kind of ‘sample bias’, or epistemic error not accounted for in linear scaling arguments, because it is not representative, even of the small-scale heterogeneity in the Earth. To overcome this Wu JY et al. (2019) carried the uniaxial and triaxial tests using fissured rock specimens with pre-existing flaws. The results show that the exponential strength criterion is more suitable than the Mohr-Coulomb strength criterion to characterize the strength characteristics of the fissured rock. The crack evolution and failure characteristics of fissured rock specimens are more complicated than those of intact rock specimens. The failure characteristics of the fissured rock follow the tensile shear coalescence model, crack branching occurs with increasing the loading rate, and the multi-section coalescence model is verified with increasing the confining pressure. The phenomena of stress drop and yield plateau usually occur after the dilatancy onset, and the specimen does not fail instantaneously. The propagation and coalescence of cracks cause a sharp increase in AE radiation, circumferential strain, and volumetric strain.

3) Granular Physics in Geophysics: Dilatancy's role in partially molten rocks and fault zone permeability under stress is being explored for its impact on seismicity and resource transport.

For example, linked with the dilatancy and slip behavior of the fault gouge as a granular material, Parez et al. (2023) focused on the effect of pore-pressure fluctuation. They pointed out that pore pressure drop at the initiation of dilatancy during accelerating slip may suppress nucleation of earthquakes known as dilatancy hardening (Segall et al., 2010; Makhnenko and Labuz, 2015; Brantut, 2020; Aben and Brantut, 2021). They suggested that the key is the critical slip rate; below and up to the critical slip rate it corresponds to the “drained” regime, in which the pore pressure drop is consistent with an incompressible fluid flow. The excess pore pressure is efficiently relaxed and has negligible effect on slip stability. In contrast, when exceeding the critical slip rate, corresponding to the onset of ‘undrained’ condition, the pore pressure drop decays slowly, inhibits dilatation rate, and significantly increases the strength of the layer, stabilizing the rupture growth. The magnitude of the pore pressure drops increases monotonically with the ratio of the dilatation rate to a characteristic fluid infiltration rate. Their results shed light on better constraining the drainage conditions associated with changes in slip rate, the magnitude of the generated pore pressure and the corresponding fault strengthening.

These advancements further enhanced the pertinence of the dilatancy theory with geotechnical engineering, earthquake mechanics, and materials science.

3.   Earthquake prediction based on the dilatancy-diffusion hypothesis

Frank (1965) was among the first to link Osborne Reynolds (1885) dilatancy theory with seismic activities in the crust and upper mantle. He emphasized the role of the fluid in some kind of time constants associated with earthquake processes. Historically, the earthquake dilatancy theory was adopted and developed in the late 1960s and blossomed in the early 1970s. One pioneer on this front is Professor Amos Nur (1938−2024) of Stanford University.

3.1   Prof. Nur and the dilatancy-diffusion hypothesis

Professor Amos Nur was a member of the National Academy of Sciences delegation to the People's Republic of China in 1976, in part because of his work on dilatancy/diffusion as China seismologists were actively working on earthquake prediction. He was a member of the Seismology Committee of the National Research Council (1974−1977) and served on the Advisory Board of the National Science Foundation for the same period. Prof. Nur’s papers represent one of the earliest and most influential efforts to integrate the term and concept of dilatancy-fluid diffusion directly into earthquake prediction studies.

With solid experimental support Nur and Simmons (1969) published the observed results that the P-wave velocity will increase when air-filled cracks become water saturated but the shear wave velocity remains unaffected by the presence of fluid. This paper laid out the foundation for Prof. Amos Nur formulated the important thought for interpreting certain geophysical phenomena, possibly prior to the occurrence of an earthquake, known as the dilatancy-diffusion hypothesis later.

In 1972 Professor Nur published the paper “Dilatancy, pore fluids, and premonitory variations of t_S/t_P travel times” in the seismology flagship journal Bulletin of the Seismological Society of America (Nur, 1972). Clearly, the travel time ratio is exactly equivalent to the velocity ratio v_P/v_S. A decrease of t_S/t_P corresponds to a decrease of v_P/v_S, and vice versa.

This 1972 paper was motivated by the report (Nersesov et al., 1969) on the t_S/t_P ratio variation prior to the occurrence of earthquakes in the Garm region, Tadzhikistan. Nur pointed out that the observed decrease of the ratio t_S/t_P can be a result of dilatancy of rocks around the focal zone, and the increase of t_S/t_P just prior to an earthquake can result from the flow of ground water into the dilatancy-formed cracks. The increasing pore pressure weakens the rock and leads to the observed failure. Nur also clearly noticed that this is of course only a possible process, not a necessary one. Many more detailed and accurate measurements of velocities and pore pressures are required to verify it. Nevertheless, the good agreement with laboratory behavior of cracks containing rocks makes this an attractive mechanism. This analysis provides the first strong evidence for the occurrence of dilatancy in situ. Dilatancy coupled with flow of groundwater in situ may play a major role in the mechanics of earthquakes, the generation of fore-, main, and aftershocks, creep, premonitory deformation, and the rupture process on the fault itself. This paper was one of the first to be put forward as a physical basis for purported earthquake precursors. The physical process of pore fluid flow and associated deformation was later named as the dilatancy-diffusion hypothesis (Scholz et al., 1973).

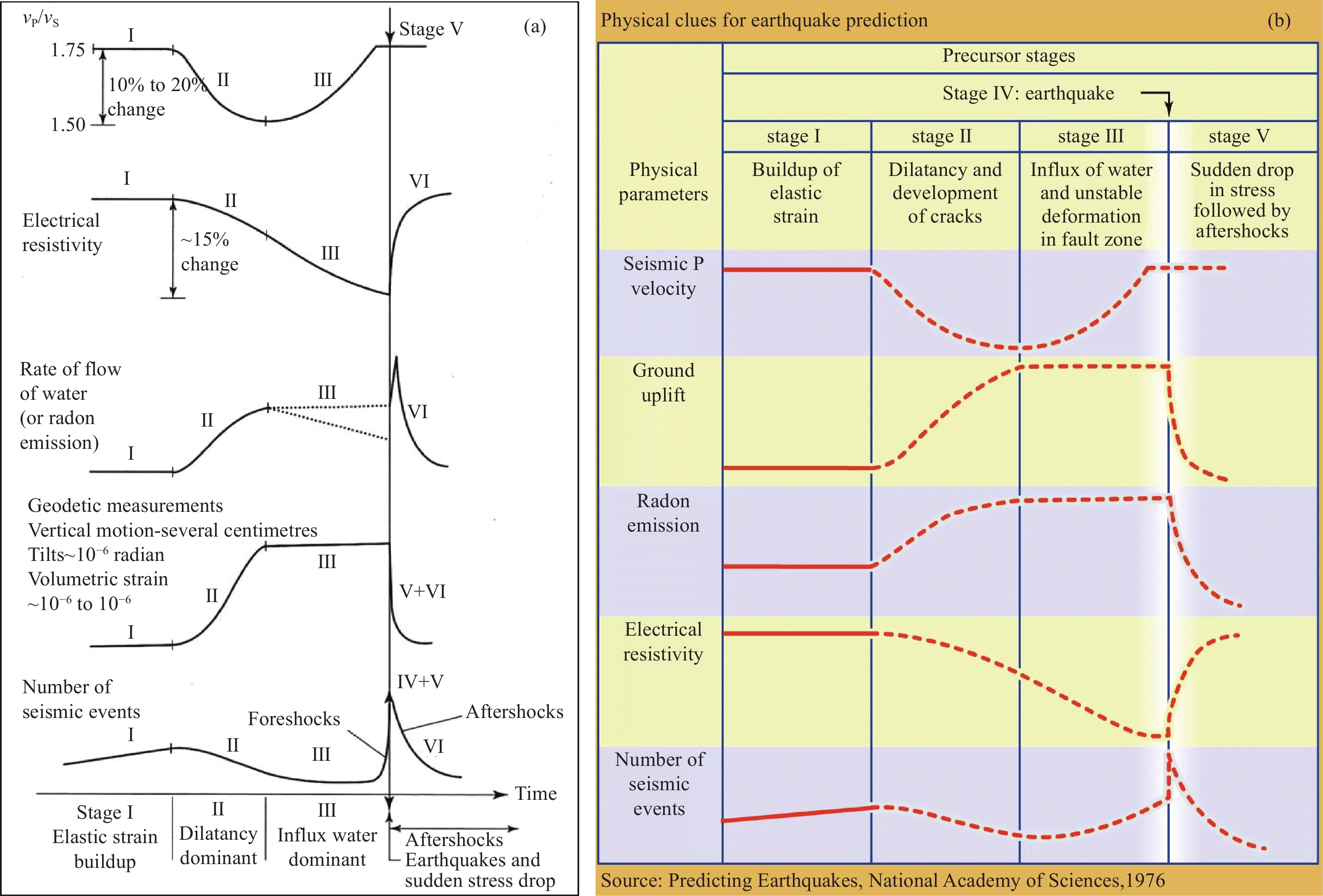
For earthquake prediction the significance of dilatancy, if real, is the effects of strain buildup on various measurable quantities of the Earth’s crust, such as seismic velocities, electric resistivity, ground deformation, gas emission, and groundwater level variations. The stages of the dilatancy process can be divided into the following phases:

1) Initial phase: As rocks begin to fracture and dilate, the pore pressure decreases because the same amount of fluid is now distributed over a larger volume.

2) Re-equilibration phase: Over time, if the rock mass is connected to a larger area filled with pore fluid, the fluid will migrate into the dilated regions, potentially increasing the pore pressure again.

3) Critical phase: High pore pressure can reduce the effective normal stress on fault planes, potentially triggering fault slip and earthquakes.

The consequences of dilatancy for earthquake prediction are summarized in Figure 3 shown as follows.

Figure  3.  Illustration of the dilatancy-diffusion model for the predictions of anomalies in geophysical signals associated with elastic loading, dilatancy, diffusion, co-seismic and post-seismic periods. (a) after Scholz et al. (1973); (b) the same model presented with a version simplified from National Research Council (1976).

DownLoad: Full-Size Img PowerPoint

In Figure 3, the best-studied consequence is the effect on seismic velocities (v_p/v_s). The influence of internal cracks and pores on the elastic properties of rocks can be clearly demonstrated in laboratory measurements of those properties as a function of hydrostatic pressure. In the case of saturated rocks, experiments predict for shallow earthquakes-that dilatancy occurs as a portion of the crust is stressed to failure, causing a decrease in the velocities of seismic waves. Recovery of velocity is brought about by subsequent rise of the pore pressure of water, which also has the effect of weakening the rock and enhancing fault slip. In a laboratory experiment Scuderi et al. (2016) systematically altered the stiffness of the loading system to reproduce the transition from slow to fast stick-slip and monitored ultrasonic wave speed during frictional sliding. They find systematic variations of elastic properties during the seismic cycle for both slow and fast earthquakes indicating similar physical mechanisms during rupture nucleation. Their data show that accelerated fault creep does cause reduction of seismic velocity during the preparatory phase preceding failure. Unfortunately, in the field at a crust scale, seismic velocity variation did not always appear in all the earthquake events with prediction effort, even other anomalies were pronouncedly presented (Nur, 1974).

Because the electrical conductivity of rocks depends largely on interconnected water channels within the rocks, conductivity may increase before the cracks become saturated. Meanwhile, as pore fluid is expelled from the closing cracks, the local water table would rise and concentrations of gases such as radioactive radon would increase.

If fluid flow increases the pore pressure back to a critical level, it can trigger fault slip, resulting in an earthquake. During an earthquake, the fault slip can cause a sudden release of stress and an increase in permeability, allowing fluids to migrate and further affect pore pressure.

Professor Nur further studied the constitutive relationship and proposed a power law form between the dilatant strain and the deviatoric stress in the paper ‘A Note on the Constitutive Law for Dilatancy’ (Nur, 1975). These relations indicate that the changes in the dilatant volume due to pre-seismic fault slip greatly depend on the dilatancy constitutive law. As creep develops with time, the 'stick' area A (like the concept of ‘asperity’ in later studies) diminishes with time. In microcrack dilatancy, the dilatant volume, which is proportional to the square root of the 'stick' area A, will increase with creep and time.

With Professor Nur’s leadership, Stanford University, along with the US Geological Survey Seismology Group of Menlo Park as the close neighbor, became one of the gravity centers for international earthquake physics studies with several critical players (Zoback and Byerlee, 1975; Segall and Simpson, 1986; Segall and Rice, 1995; Townend and Zoback, 2000; Zoback, 2006; Lockner et al., 2011; Segall and Brodley, 2012; Proctor et al., 2020; Cattania and Segall, 2021) in the team. In the same period scientists from other institutions (Anderson and Whitcomb, 1973; Whitcomb et al., 1973; Aggarwal et al., 1973; Scholz et al., 1973; Anderson and Whitcomb, 1975; Brace,1975; Freudenthal, 1975; Scholz, 1977) worked parallelly and mutually developed the dilatancy-diffusion hypothesis to the maturity of what we know today.

The dilatancy-diffusion hypothesis has been utilized in interpreting certain earthquake sequences, though its success has been mixed and context-dependent. However, the theory provides a framework for understanding the physical processes leading up to earthquakes and has contributed to predictive efforts. Here are a few examples where dilatancy-diffusion hypothesis has been employed to interpret the observed anomalous phenomena prior to an earthquake.

3.2   Prediction effort prior to the 1975 Haicheng Earthquake

According to reports and re-count of the reports, along with person-to-person interviews there were numerous observed anomalies and unusual animal behavior occurred before th1975 Haicheng Earthquake (Wang KL et al., 2006). As early as 1970, the State Seismological Bureau (now the China Earthquake Administration) had identified the Liaoning Province as an area of high seismic risk. According to Liaoning Provincial Seismological Bureau, beginning in September of 1973, there had been reports on numerous anomalies in short term water levels, seismicity and radon gas content in groundwater in Jin County. Using deep learning methods Liu ZM et al. (2025) picked P- and S-wave phases from continuous waveforms recorded by a network containing 52 stations with 150 km radius centered at Haicheng city from January 2018 to July 2020. The seismicity relocation results re-confirmed that the 1975 Haicheng Earthquake did occur on the WNW oriented Haicheng-Dayanghe Fault.

In June 1974, a little more than six months before the earthquake struck, there was a flurry of small earthquakes in the region. Based on this activity, an official State Council report was made that a magnitude 5−6 earthquake might occur in the northern Bohai area in the next 1−2 years. Also, gravimeter surveys that had been carried out in the region earlier in 1972 and 1973 (Chen YT et al., 1979), had revealed considerable variations in gravity values, however with no explanation of their significance. In the next few months of 1974, there were numerous additional abnormal phenomena and deformation in the eastern Liaoning Peninsula area, such as changes in land elevation and in ground water levels. The regional increase in seismicity triggered a low-level alert. This activity occurred near the cities of Haicheng and Yingkou. Undoubtedly, the most relevant factor to the dilatancy-diffusion hypothesis, and the most important phenomenological support for the low-level alert issued, were these foreshock sequences.

Abnormal earthquake activity in the Haicheng area intensified on February 3,1975. On February 4, the day of the earthquake, based primarily on the observed unusual behavior of animals, a local county government authority issued a specific evacuation order for the immediate area. Based on these warnings that were issued about five and half hours prior to the event, a massive evacuation began in the afternoon to early evening. However, the evacuation was extremely uneven across the region, as critical decisions to evacuate or not were made unilaterally by the grass-root local authorities and by individual citizens acting spontaneously and independently. Nonetheless, these evacuation actions helped save thousands of lives. Another important factor is the timing of the earthquake at 19:36 in the evening contributed to minimizing the overall death toll, since most people were still awake for daily activities.

The apparent success of the prediction of the Haicheng Earthquake generated a period of optimistic hope for earthquake prediction (Press, 1975; Adams, 1976; National Research Council, 1976) and attracted much attention from seismologists all over the world to visit the Haicheng earthquake epicentral area. As one of the members of the US National Academy of Sciences delegation Professor Nur visited Haicheng in 1976 (Raleigh et al., 1977). The National Research Council Panel on Earthquake Prediction made a report based on this visit and made an optimistic evaluation of the future of earthquake prediction (National Research Council, 1976) The report stated that ‘Anomalous physical phenomena precursory to some earthquakes have been clearly identified.’ and ‘A scientific prediction will probably be made within the next five years for an earthquake of magnitude 5 or greater in California. With appropriate commitment, the routine announcement of reliable predictions may be possible within 10 years in well-instrumented areas.’ However, the panel clearly identified the importance of the role of government organizations and societal responses to the outcome of a prediction. Based on their personal observation and perception at the site of the Haicheng Earthquake the report also emphasized the critical role of societal response by stating that ‘A prediction capability will be of little value if societal response procedures are not formulated concurrently’.

On the critical issue of the fore-shock and mainshock relationship, Jones et al. (1982) noted that the radiation patterns can tentatively be correlated with various parts of the zone. The hypocenter of the mainshock was not located on the same fault as that defined by the foreshocks' hypocenters but instead was located 6 km south of and several kilometers shallower than the foreshock cluster. They think this large separation between foreshocks and mainshock in a direction perpendicular both to the plane of rupture of the mainshock and to the trend of the foreshocks might be the result of an en echelon step in the fault that slipped during the mainshock. An analysis of the change in stress due to slipping during the foreshocks shows that the increase in shear stress on the mainshock fault caused by the foreshocks is very small and that direct triggering of the mainshock by the foreshocks is unlikely.

Moreover, many heavily cited anomalies or ‘precursors’ in the literature of Haicheng Earthquake prediction are actually reported retrogradely after the earthquake occurrence (Duan XB et al., 1976; Feng R et al., 1976; Chen YT et al., 1979; Jiang XE and Chen FB, 1981; Xu SX et al., 1982; Jin AS and Aki, 1986; Mogi, 1987; Wang LY et al., 2008; Rohrbach et al., 2013; Lei XL et al., 2024). Thus, they bear less credibility due to their non-robustness to stand up with more rigorous scrutiny such as the ‘double blind’ test, which serves as the standard and only acceptable method of testing in medical sciences (Modell and Houde, 1958). Furthermore, under the dilatancy-diffusion hypothesis and put into the rigorous criteria guidelines for precursor candidates proposed by IASPEI (Wyss and Booth, 1997) as: (1) the physical model relating the precursor to the main shock, and the amplitude-distance variation of the anomaly associated with the precursor, including independent evidence for especially sensitive observation sites; (2) the data, such as instrument positions and calibration, associated editing criteria; (3) anomaly definition (so that other data sets can be examined for anomalies); and (4) the rules and reasons for associating a given anomaly with a given earthquake. Few of the reported ‘precursory’ anomalies have survived the rigorous, independent scrutiny based on these criteria (Geller, 1997).

Conclusively, Wang KL et al. (2006) made a diligently detailed inventory of all the facts pertinent to the handling of the precursory reports prior to the occurrence of the mainshock at 19:36, February 4, 1975. They concluded that ‘Although the prediction of the Haicheng earthquake was a blend of confusion, empirical analysis, intuitive judgment, and good luck, it was an attempt to predict a major earthquake that for the first time did not end up with practical failure’.

Dramatically enough, the optimistic-toned National Research Council (1976) report was published in July 1976, ironically, only a few days before the tragic Tangshan Earthquake occurred on July 28, 1976. Along with some unsuccessful prediction attempts (e.g., Bakun et al., 2005) the perception to the feasibility of earthquake prediction was changed in the seismological community, forcing the entire to re-evaluate the approach to conducting seismic hazard reduction studies (Wang KL et al., 2006; Main et al., 2012)

Anyway, it is noteworthy to point out that some researchers are consistently practicing earthquake prediction. Pritchard et al. (2020) discussed the status and further possibility to simultaneously detect earthquake foreshocks and slow-slip phenomena through ground deformation, seismic, and gravitational transients—weeks to months before large subduction zone earthquakes. As the latest development, artificial intelligence (AI) started to play more roles in scientific research (Tokuda and Shimada, 2019; Banna et al., 2020; Tehseen et al., 2020; Saad et al., 2023; Ridzwan and Yusoff, 2023; Zhu GH et al., 2025). For example, using a machine learning approach Zhu GH et al. (2025) detected anomalous hydrochemical signatures from 6 hot springs located in southeast China, aiming to search the correlations with the occurrence of mostly Taiwan earthquake events. Saad et al. (2023) trained machine learning algorithms (principal component analysis and random forest) with five years of seismic recordings and then asked them to locate upcoming quakes based on current seismic activity. The authors claimed that the AI algorithm can correctly predict 70 percent of earthquakes one week before they happened.

4.   The inability of the dilatancy-diffusion hypothesis for earthquake prediction

As we have shown in the previous sections the dilatancy-diffusion hypothesis was one of the first attempts to predict the form of potential geophysical anomalies that may precede earthquakes and hence provided a possible physical basis for earthquake prediction. The basic hypothesis has stood up well in the laboratory, where cascadic failure of intact rocks has been observed that can be associated with geophysical signals associated with both dilatancy and pore pressure variations. In contrast, at the field scale, it has provided insights into a small number of earthquake sequences, but its application has failed to lead to successful predictions in most occurrences. The ultimate reason is that the heterogeneity of geological conditions and the multifaceted nature of fault systems prevent the dilatancy-diffusion hypothesis from being universally applied to all cases.

4.1   Factors hindering dilatancy-diffusion for effective earthquake prediction

The inability of the dilatancy-diffusion hypothesis to interpret all geophysical anomalies of crustal earthquakes was due to a number of reasons. The most critical one is the complexity and non-linearity of earthquake processes. The mechanical behavior of the solid skeleton of crustal rocks is complicated. In contrast, the behavior of fluids in the crust is much more complicated due to their fluidity. Thus, the response of rocks as multi-phase media to the loading stresses is extraordinarily complex and variable, making it difficult to consistently identify and interpret precursory phenomena based merely on the dilatancy-diffusion hypothesis alone.

Main et al. (2012) pointed out that the huge scale difference between laboratory experiments and earthquake prediction in the field is the key hindering us from understanding the physics of seismogenic process. The scale difference is twofold: in space and in time. The difficulty of upscaling the dilatancy-diffusion hypothesis spatially is relatively straightforward to understand. Though we can have detailed information on material texture, structure and fracture for a rock sample for laboratory tests, it is impossible to acquire the same information, at the same level of resolution of the Earth material at a size of tens to hundreds of kilometers. Certain kinds of idealization or conceptualization must be taken to generate a model of Earth material at that size. Even though we can use all kinds of tomographic imaging approaches, we can never reach the resolution of the structural features we have gotten from the laboratory samples. Uncertainties and complexities thus emerged from spatial upscaling. Simply due to the fact that we are not observing fault processes at the necessary scale and resolution, this is why the search for evidence of dilation-related precursors from geophysical data in natural systems has largely failed (Main et al. 2012; Caniven et al., 2021).

From the time scaling point of view, the generally accepted inter-seismic crustal strain rate is about 10⁻¹⁷ to 10⁻¹⁵ per second in intraplate regions, with 10⁻⁹/s as the extreme to be found at deformation centers such as the plate boundary collision zones, based on global GPS network observations (Kreemer et al., 2014). In contrast, typical laboratory tests at constant strain rate loading are of the order 10⁻⁵/s. A very slow ‘creep’ test (loaded with constant stress) that takes weeks to months, can slow down the strain rate to 10⁻⁸/s. It is therefore quite possible that different physical and physico-chemical processes may actually be involved across these enormous ranges.

Other factors that hinder us from better understanding earthquake physics include the complex and chaotic nature of earthquake processes beyond the dilatancy-diffusion process and the incompleteness of data coverage. For example, in the time domain we can never get a uniformly complete earthquake catalog for thousand years, even for the seismic active areas with the best historic records. In the space domain, social and economic constraints, as well as geopolitical borders prevent us from constructing dense and uniformly distributed monitoring networks in earthquake-prone regions. Bletery and Nocquet (2023) conducted a global search for short-term precursory slip in GPS data. During a 48-hour time window directly before 90 M_W≥7 earthquakes they examined the displacements measured by 3026 high-rate GPS time series and projected them onto the directions expected from precursory slip at the hypocenter. Their result revealed a 2-hour-long exponential acceleration of slip directly before the ruptures. The result suggests that large earthquakes start with a detectable precursory phase of slip merely two hours before the mainshock. This result implies that only a densely sampled, in both space and time, with high precision observation network can capture this credible subtle anomaly as the true precursor.

4.2   Dilatancy-diffusion hypothesis and earthquake nucleation

Along the course of the development of earthquake physics the dilatancy-diffusion hypothesis is followed by the earthquake nucleation theory (Brace and Byerlee, 1966; Das and Scholz, 1983; Ellsworth and Beroza, 1995; Beroza and Ellsworth, 1996; Harbord et al., 2017; Scholz, 2019; Lebihain et al., 2021; Peng ZG and Lei XL, 2024; Sornette et al., 2024). The nucleation theory included more time-dependent mechanisms like rate and state friction (RSF) in its physical description of earthquake preparation for the phase directly prior to and co-temporal of the dynamic rupture stage of an earthquake. In general, dilatancy should be considered as a quasi-static preparatory stage that occurred prior to the dynamic rupture nucleation within a smaller region. Dilatancy leads or triggers the nucleation of a rupture. The rupture then propagates on fault planes, potentially involving a much larger area than the initial dilatant zone. Zhu GH et al. (2025) reported a case of the 2016 M_S5.1 Yunlong earthquake in Western Yunnan, China. Although the earthquakes in this region exhibit a cascade process in nucleation, the established temporal transient in b-value shows precursory drops, which is optimistic for probabilistic short-term hazard warnings in the region.

The rupture zone is much larger than the initial dilatancy area and can reach Earth surface under certain conditions. Therefore, while dilatancy-diffusion is a crucial precursor, it affects a smaller area than the final rupture zone. To the first order of simplification we can see that the dilatancy-diffusion period has a longer time scale; it is possible to grant us the needed time to observe and react. However, the much smaller region in certain depth of the crust makes direct observations extremely hard. In contrast, the dynamic rupture nucleation occurs in a much larger region but with short to almost no time for us to react in terms of precursor identification and issuing prediction. Combination of the dilatancy-diffusion and the nucleation enable us to envision a much complete picture of the seismogenic process, but nucleation theory’s contribution to prediction or forecasting is limited.

In summary, while the dilatancy-diffusion hypothesis and the rupture nucleation can provide valuable insights of earthquake physics, predicting earthquakes based on precursors remains highly challenging to almost impossible due to the complex and variable nature of fault a system. Other approaches must be sought to put the dilatancy-diffusion hypothesis to a smarter use, as described in the next section.

5.   Operational earthquake forecasting and deep learning

5.1   Operational earthquake forecasting (OEF)

In general prediction can be defined as the act of making an educated guess or estimation about a future event or outcome with or without relying on extensive historical data or patterns. It involves using available information, knowledge, and expertise to anticipate what might happen in the future. Prediction often relies on expert judgment, intuition, and qualitative analysis rather than quantitative data and statistical models. It incorporates subjective assessments, qualitative reasoning, and domain-specific knowledge to make informed predictions about future events or outcomes. Essentially, prediction is deterministic without giving a level of confidence or statistic error bar.

In contrast, forecasting is a systematic process of estimating or predicting future outcomes or events heavily based on historical data, patterns, and trends. Its purpose is to provide insights and projections to guide decision-making, planning, and resource allocation. Forecasting involves analyzing historical data and employing various statistical and mathematical techniques to identify patterns and trends. Time series analysis, regression analysis, and machine learning algorithms are commonly used to forecast future values based on historical data. Current weather forecasting can be named as the best example of forecasting practice.

In short, a prediction is defined as a deterministic statement that a future earthquake will or will not occur in a particular geographic region, time window, and magnitude range, whereas a forecast gives a probability (greater than zero but less than one) that such an event will occur. This probabilistic essence for dealing with the risk of a pending earthquake has been recognized by scientists (e.g., Turcotte, 1991) for quite some time before an operational approach as described as follows.

Following the 2009 L'Aquila earthquake (Amoruso and Crescentini, 2010), the Dipartimento della Protezione Civile (DPC) of Italy appointed an International Commission on Earthquake Forecasting for Civil Protection (ICEF) to report on the current state of knowledge of short-term prediction and forecasting of tectonic earthquakes and indicate guidelines for utilization of possible forerunners of large earthquakes to drive civil protection actions, including the use of probabilistic seismic hazard analysis in the wake of a large earthquake. The ICEF reviewed research on earthquake prediction and forecasting, drawing from developments in seismically active regions worldwide. This is the start of the framework now known as the operational earthquake forecasting or OEF (Jordan et al., 2011; Mizrahi et al., 2024).

OEF is the real-time assessment and communication of the probability of future earthquakes in a specific region and timeframe, typically spanning days to weeks. It integrates short-term seismic activity (e.g., foreshocks or aftershocks), geophysical data, and statistical models to provide actionable insights for decision-making related to hazard mitigation and public safety.

Long-term models adopted by OEF are currently the most important forecasting tools for civil protection against earthquake damage, because they guide earthquake safety provisions of building codes, performance-based seismic design, and other risk-reducing engineering practices, such as retrofitting to correct design flaws in older buildings.

On short time scales of days and weeks, earthquake sequences show clustering in space and time, as indicated by the aftershocks triggered by large events. Statistical descriptions of clustering explain many features observed in seismicity catalogs, and they can be used to construct OEF forecasts to indicate how earthquake probabilities change over the short term. If properly applied, short-term forecasts have operational utility, e.g., for foreseeing aftershocks following large earthquakes. In contrast to the better received value of long-term forecasts for ensuring seismic safety, the interpretation of short-term forecasts is problematic, because earthquake probabilities may vary over orders of magnitude but typically remain low in an absolute sense (< 1% per day). Indeed, translating such low-probability forecasts into effective decision-making is a difficult challenge in OEF (Jordan et al., 2011).

OEF intends to provide the public with open sources of information about the short-term probabilities of future earthquakes that are authoritative, scientific, consistent, and timely. Advisories should be based on operationally qualified, regularly updated seismicity forecasting systems that have been rigorously reviewed and updated by experts in the creation, delivery, and utility of earthquake information. The quality of all operational models should be evaluated for reliability and skill by retrospective testing, and they should be under continuous prospective testing against established long-term forecasts and alternative time-dependent models. Alert procedures should be standardized to facilitate decisions at different levels of governing bodies and among the public. Earthquake probability thresholds should be established to guide alert levels based on objective analysis of costs and benefits, as well as the less tangible aspects of value-of-information, such as gains in psychological preparedness and resilience. The principles of effective public communication established by social science research should be applied to the delivery of seismic hazard information (Mizrahi et al., 2024).

To enhance its capability, OEF system is increasingly adopting deep learning (DL) to improve accuracy and efficiency. Though statistical models are the backbone for OEF, through deep learning, especially by using the physically-informed neural networks (PINNs), physical models, such as the dilatancy-diffusion theory, to make the forecasting with more enhanced physical basis.

5.2   Deep learning with physically-informed neural networks (PINNs)

Deep learning (DL) models are good at learning complex non-linear patterns when there are large amounts of data (Eghbalian et al., 2023; Fukushima et al., 2023; Dascher-Cousineau et al., 2023; Liu MP et al., 2024). Most physical systems have too many nonlinear interactions like friction, slipping, pore fluid flow and transport etc. Capturing them all with physics equations is hard and tedious. Thus, a simplified physics representation of the system in combination with deep learning process enables one to model the observed error between the simplified physics and the true system. Combination of the simplified physics system and the DL model can create a more accurate, and more physically-sound representation of the real system. The physically-informed neural networks (PINNs) technique is an ideal tool to realize this combination.

PINNs have gained much popularity due to its advantage of combining the data-driven approach with the first principle physical laws to assure physically sound solutions (Okazaki et al., 2022). This approach bridges the gap between data-driven methods and physics-based models, offering a more robust framework for solving scientific and engineering problems. This approach is through the construction of the physics-guided loss functions. Instead of purely minimizing the difference between predicted and observed data, PINNs include terms in the loss function that penalize violations of physical laws (e.g., conservation of energy, momentum, etc.). PINNs require less experimental or observational data compared to purely data-driven models because they rely on physics to fill in gaps where data is sparse. PINNs train the network by minimizing a combined loss: one part from data and another from the physical equations. It incorporates domain knowledge, improving generalizability and reliability; works well in scenarios with limited or noisy data and can provide physically consistent forecasting.

In earthquake physics, Fukushima et al. (2023) proposed a PINN-based new approach to simulate fault slip evolutions, estimate frictional parameters from observation data, and predict subsequent fault slips. As the first step, they validate the effectiveness of the PINN-based approach using a simple single-degree-of-freedom spring-slider system to model slow-slip events. As a forward problem, they successfully reproduced the temporal evolution of slow-slip events using PINNs and obtained implications on how to choose the appropriate collocation points by analyzing the residuals of physics-based differential equations. As an inverse problem, they estimated the frictional parameters from synthetic observation data and demonstrated the ability to obtain accurate values regardless of the choice of first-guess values. Furthermore, they discussed the potential of the predictability of the subsequent fault slips using limited observation data, considering uncertainties. Their results demonstrated the significant potential of PINNs for fault slip monitoring.

Structural failures are often caused by catastrophic events such as earthquakes and winds. Consequently, it is crucial to predict dynamic stress distributions during highly disruptive events in real time. Currently available high-fidelity methods, such as finite element models (FEMs), suffer from their inherent high complexity. Therefore, reducing computational cost while maintaining accuracy is highly desired. Bolandi et al. (2023) proposed a PINN-Stress model to predict the entire sequence of stress distribution based on finite element simulations using a partial differential equation (PDE) solver. Using automatic differentiation, they embed a PDE into a deep neural network’s loss function to incorporate information from measurements and PDEs. The PINN-Stress model can predict the sequence of stress distribution in almost real-time.

Expanding from pure elastic to elasto-plastic media Liu MP et al. (2024) presented a PINN study case that captures the elasto-plastic behavior of soils under complex strain and stress paths. The PINN uses the void ratio and plastic strain as the outputs of the neural networks and then includes them in a general elasto-plastic stress-strain relationship as an additional loss function. The PINN provides a more stable prediction and a superior performance than deep neural networks in forecasting the stress, strain, plastic strain, and void ratio. The PINN was then incorporated into a finite element framework as a replacement for the constitutive model to solve boundary value problems. Three cases, biaxial test, layered-soil compression, and cavity expansion, showed that the finite element-PINN framework results in excellent agreements of deviatoric stress, plastic shear strain, and void ratio compared to state-of-the-art numerical methods as a benchmark. The approach captures the stress-history memory of soils as well as the volumetric and shear response of soil, including contractive and dilative behavior. The stress concentration and strain localization characteristics were also reproduced by the finite element-PINN framework in the boundary value problems. Critically this approach also achieves outstanding performance in plasticity without the need to define plastic yield functions or hardening rules.

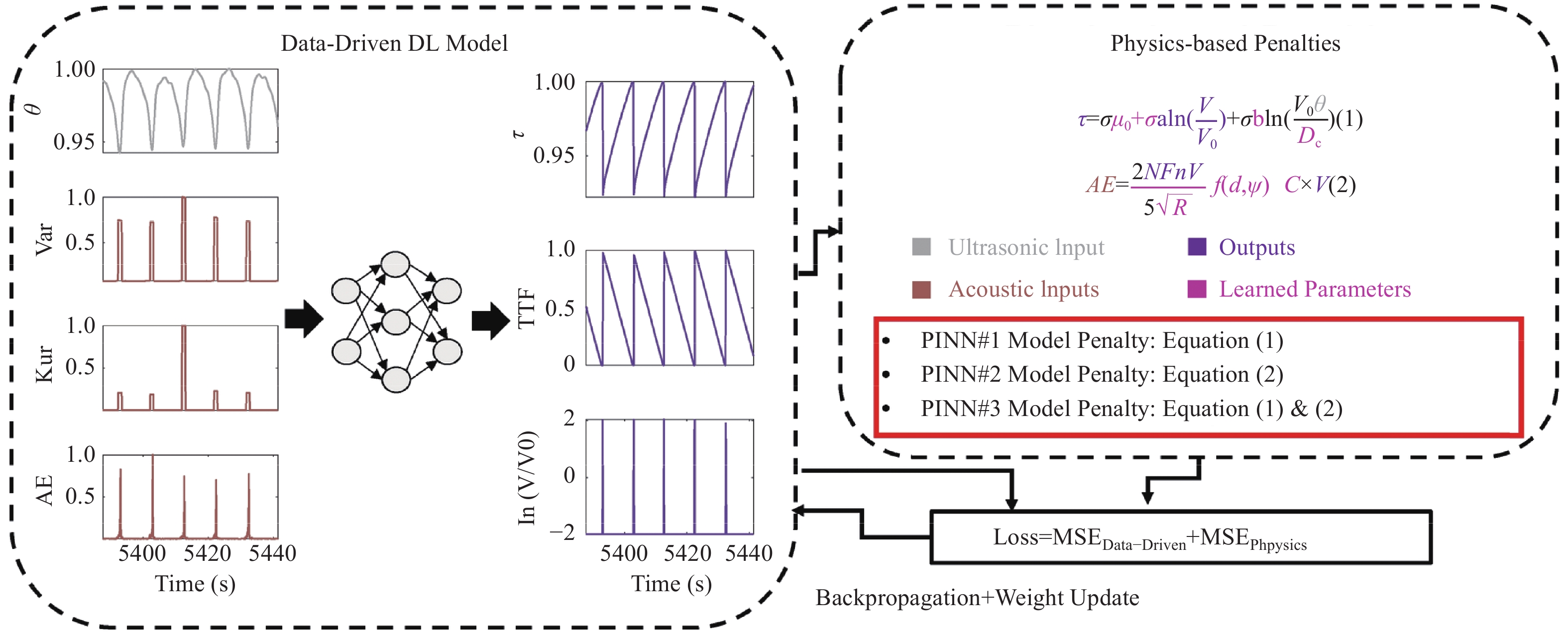
By inclusion of more sophisticated fracture nucleation constitutive relation Borate et al. (2024) used data from shear experiments coupled with passive acoustic (variance, kurtosis, and acoustic emission (AE) rate) interleaved with active source ultrasonic monitoring (transmitted wave amplitude) to develop PINN models incorporating the RSF law and AE rate generation equation with wave amplitude serving as a proxy for friction state variable. This PINN framework allows learning RSF parameters from stick-slip experiments rather than measuring them through a series of velocity step experiments. When the stick-slip cycles are irregular, Borate et al. (2024) found that the PINN models can outperform pure data-driven DL models. The next figure (Figure 4) is the setup of PINNS adopted by Borate et al. (2024).

Figure  4.  Schematic representation of the PINN framework developed for shear stress, time to failure, and slip rate prediction using active-passive data. Three PINN models were penalized by rate and state law and AE rate generation equation (Figure 5 of Borate et al. 2024).

DownLoad: Full-Size Img PowerPoint

It is worth taking the dilatancy-diffusion hypothesis as the physical model into PINNs to expand the OEF models, because it emphasizes the interplay between stress, deformation, fluid movement, along with its capability to link with other geophysical fields as observables. Its intrinsic substance cannot be replaced by other seismogenic hypotheses. Lyakhovsky and Ben-Zion (2020) presented an encouraging result from a semi-analytical and numerical analysis to show that even for a typical rupture zone (faults) with a thin tabular geometry, the expected small aspect ratio explains the general seismological observations of small isotropic radiation. However, isotropic radiation induced by dynamic dilation for short and thick sources is more pronounced and may reach for spherical sources sustaining shear deformation 18 per cent of the shear components. Thus, sources that include certain tensile components can produce larger isotropic radiation. The results provide rigorous relations that can be used to estimate different source properties in numerical simulations, experiments and field studies. Naturally, along the same line of evidence one can also be hopeful to see radiation of precursory information from the concentrated, small sized tabular asperities (Main et al., 2012).

Based on the above discussion, I speculate it is possible to include the dilatant-diffusion hypothesis into the PINNs model only considered the nucleation stage (Figure 4). The expansion of the more comprehensive PINNS should include the dilatancy-induced pore-fluid diffusion equation, the rate-and-state friction law, and couple with stress diffusion. The modified loss function now should include the terms arose from the newly included diffusion equations (pore-pressure and stress), the slips, and boundary conditions. This will be composed into an overly complicated system and better start from the laboratory scale, then expand to an in-situ, meso-scale test site. The issue of defining a proper boundary condition to this system is critically important; this importance increases along with the increase of the scale of the model.

Training PINNs can be more expensive than conventional neural networks. Moreover, the complex, multi-input loss function might lead to difficulties in optimization; it requires a good understanding of the underlying physical system to define appropriate constraints. By combining physical insights with data-driven statistical modeling, deep learning, especially PINNs, can be viewed as a powerful tool for advancing earthquake forecasting and improving risk mitigation strategies.

6.   Conclusions

The dilatancy theory originated in geotechnical engineering to treat the deformation of granular materials. It is supported by sound theoretical basis, laboratory experiments, and numerical simulations. The dilatancy theory has been successfully introduced into hard rock geomechanics to describe similar physical processes of rock failures. The dilatancy theory was expanded as the dilatancy-diffusion hypothesis in 1960s to 1970s for the purpose of interpreting earthquake precursors that occurred before an earthquake with the objective of earthquake prediction. However, while the dilatancy-diffusion hypothesis has contributed to understanding earthquake precursors and has successfully predicted a few small earthquakes, in general it cannot stand up to rigorous independent scrutiny when attempt to predict other larger events. The main reason is the nonlinearity and complexity in time and space when upscaling the problem from laboratories to the Earth crust. Nevertheless, the dilatancy-diffusion hypothesis is the most comprehensive theoretical framework to interpret the seismogenic process in the Earth crust. Given the fact of the scientific community’s realization of the prediction appears to be a ‘Mission Impossible’ at the current level of understanding (or ‘un-understanding’) of the seismogenic process and shift to operational earthquake forecasting (OEF), the dilatancy-diffusion hypothesis can be one of the most ideal candidates to serve as one of the physical models in deep learning algorithms using the physically-informed neural networks (PINNs). We are happy to see that strong and accelerated developments on this front have emerged in literature. The seismological community should continue improving the operational earthquake forecasting (OEF) to reduce the seismic risk and save countless lives.